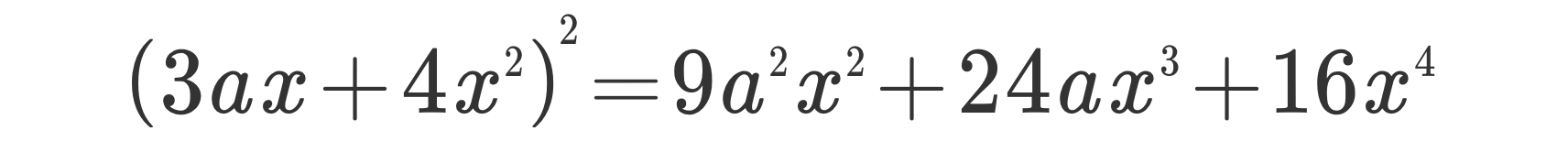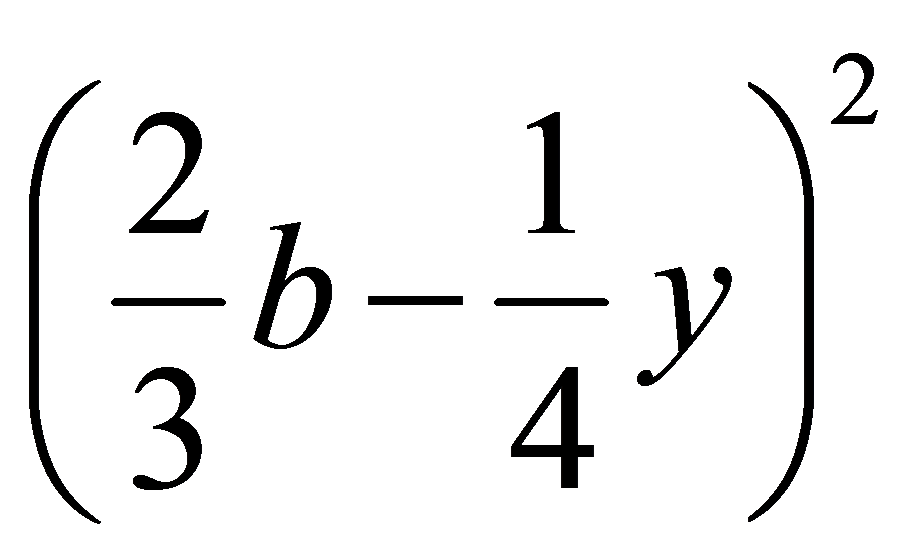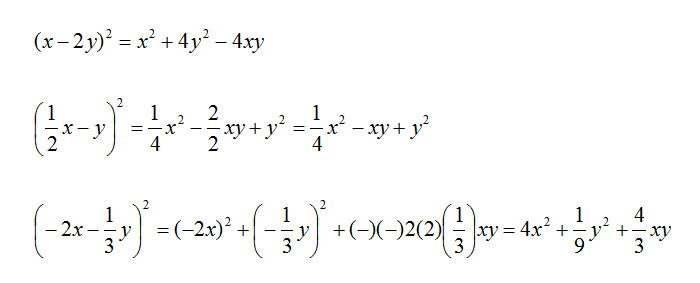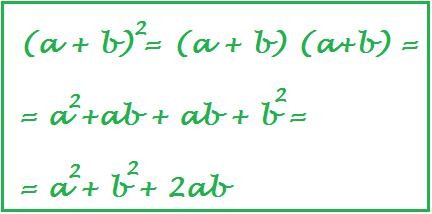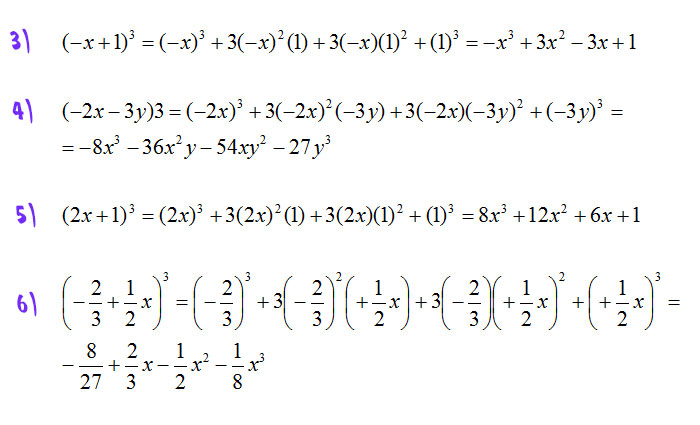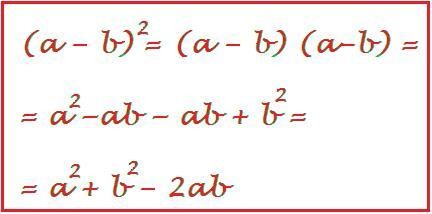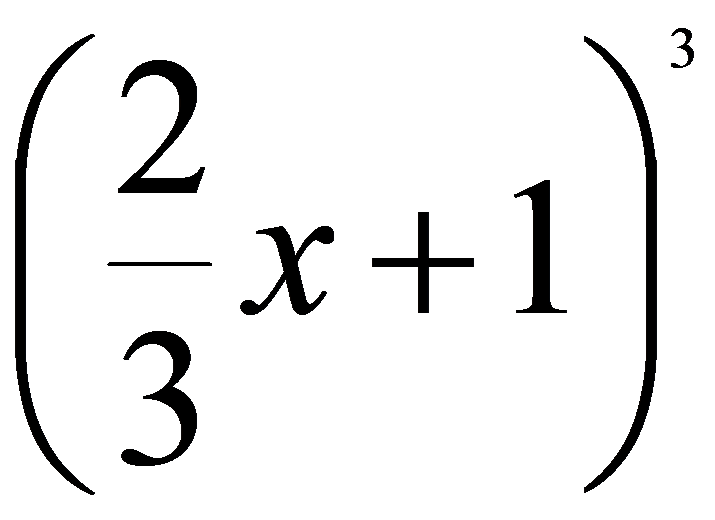Quadrato Di Un Binomio

Per la lezione di riepilogo sui.

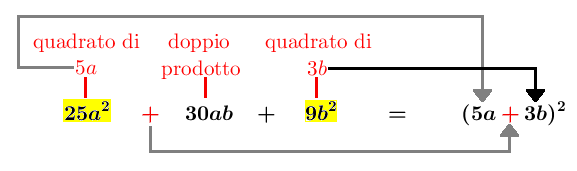
Quadrato di un binomio. Salvo casi fortuiti o particolari quando si calcola il quadrato di un binomio si giunge alla somma di tre monomi. Realizzato con geogebra4 da marcello pedone marcellopedone tin it. Il quadrato di un binomio è un prodotto notevole che permette di sviluppare il quadrato di un polinomio con due termini. Insieme vengono elevati al quadrato.

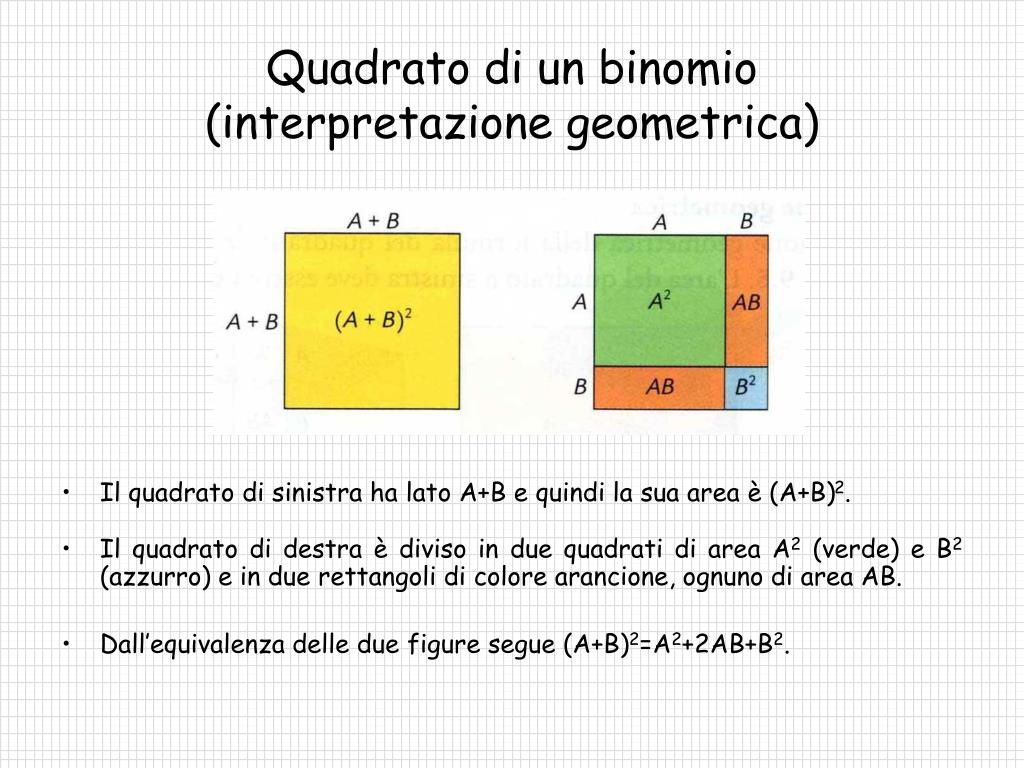
Basta moltiplicare la parentesi per se stessa così da ottenere la formula risolutiva. Spiegazione geometrica del quadrato di un binomio. Come primo esempio di sviluppo del quadrato di un binomio vogliamo calcolare. Essa ci dice che il quadrato di un binomio è uguale al quadrato del primo piu il quadrato del secondo piu il doppio prodotto del primo per il secondo.

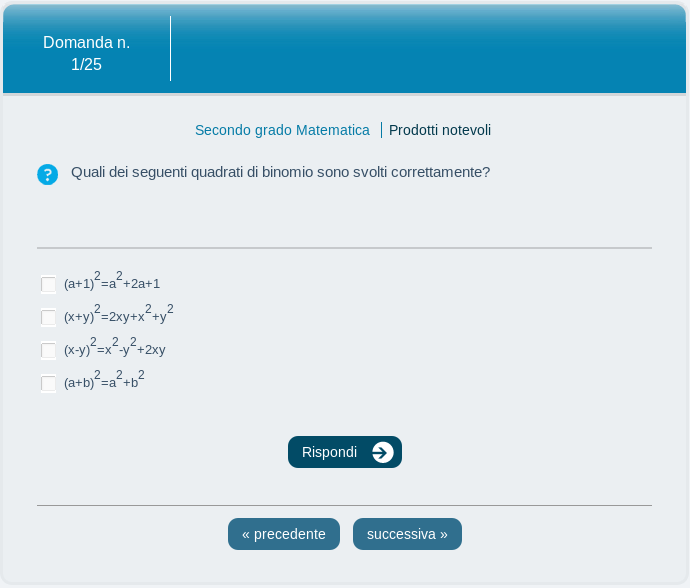
Quadrato di un binomio. X 1 2 è un quadrato di binomio con segno meno la cui formula generale che permette di scriverne lo sviluppo è. 4x 2 quadrato del secondo. Pertanto per sviluppare x 1 2 basta sostituire nella formula precedente a con x e b con 1.

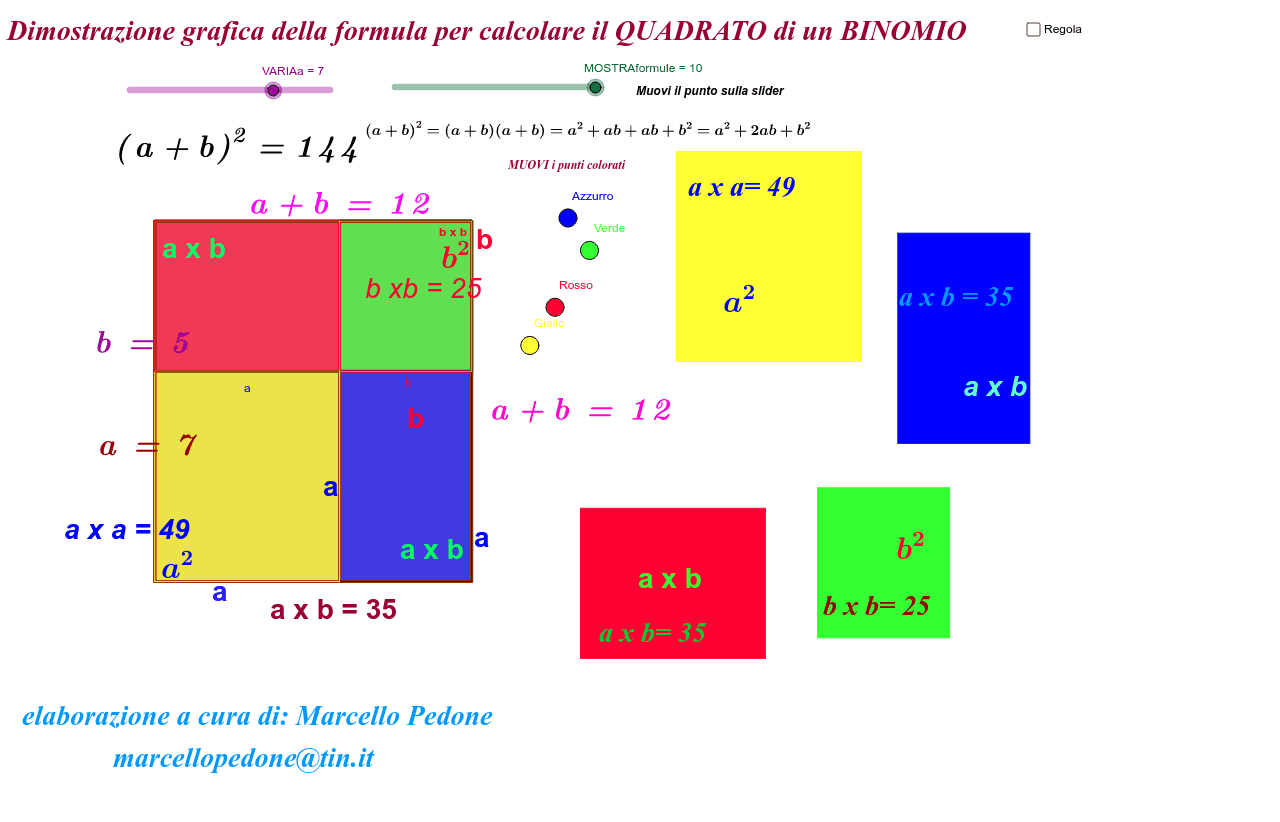
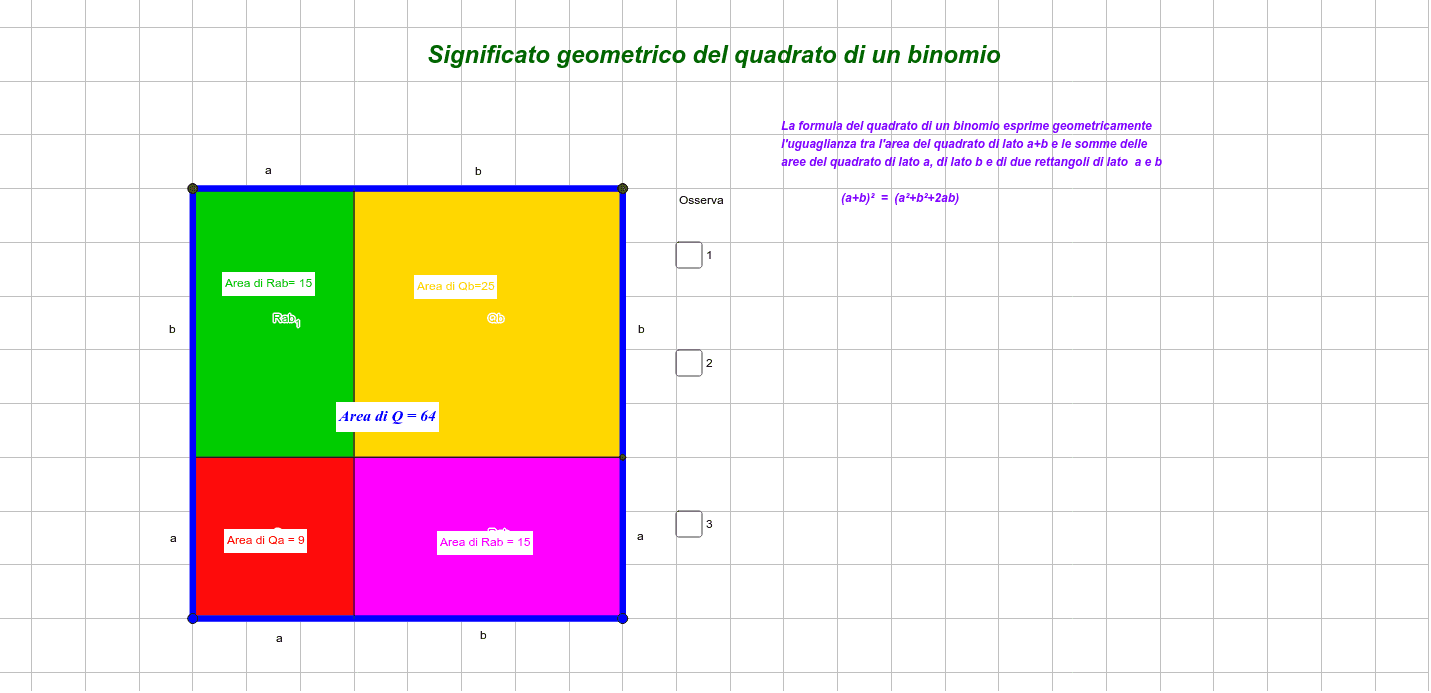
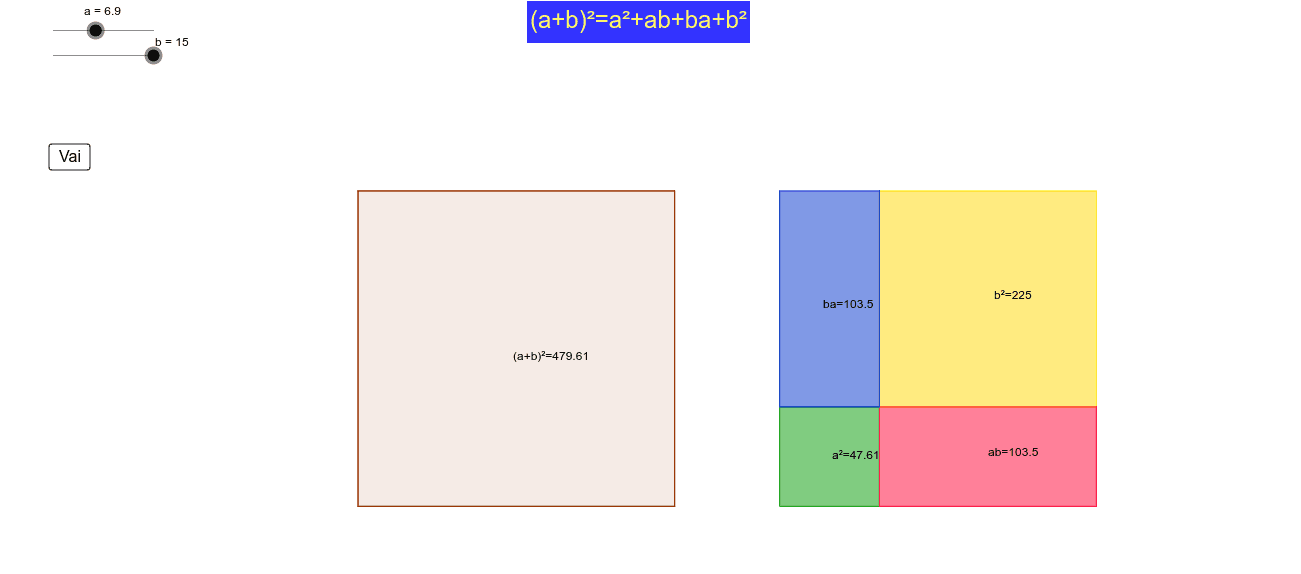
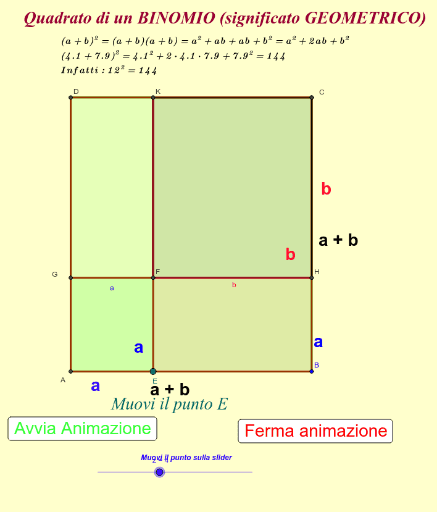
Il quadrato di un binomio e uguale al quadrato del primo monomio piu il doppio del prodotto del primo per il secondo piu il quadrato del secondo se hai bisogno di aiuto per leggere la regola fai click qui. Le due regole precedenti possono essere sintetizzata in una sola regola che prende il nome di quadrato di un binomio. Il quadrato di un binomio. Significato geometrico muovere il punto sulla slider e successivamente il punto e.

E un modo quindi per semplificarci la vita e ridurre il numero di moltiplicazioni e più in generale di operazioni. Il quadrato di binomio è un prodotto notevole che permette di sviluppare il quadrato di un polinomio a due termini ovvero una cosa del genere. Dimostrazione del quadrato di un binomio. Muovere il punto sulla slider e successivamente il punto e.

2x y 2 quadrato del primo. Il quadrato di un binomio coincide con il quadrato del primo termine più il doppio prodotto del primo termine per il secondo cui bisogna aggiungere il quadrato del secondo termine. è sufficiente sviluppare i conti con tutti i passaggi per verificarlo. Come dicevamo si tratta di un prodotto notevole perché ci evitiamo ben due passaggi semplicemente ricordando la regola del quadrato di binomio.

Esempio di sviluppo del quadrato di un binomio. Regola del quadrato di binomio. La regola del quadrato di binomio si dimostra in maniera molto semplice. Trasformazione con matrice a determinante nullo.

Anche in questo caso per verificare che quanto ottenuto è corretto calcoliamo il seguente prodotto.