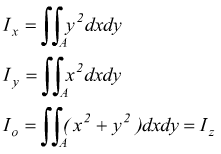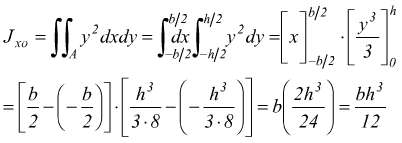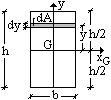Momento Di Inerzia Quadrato

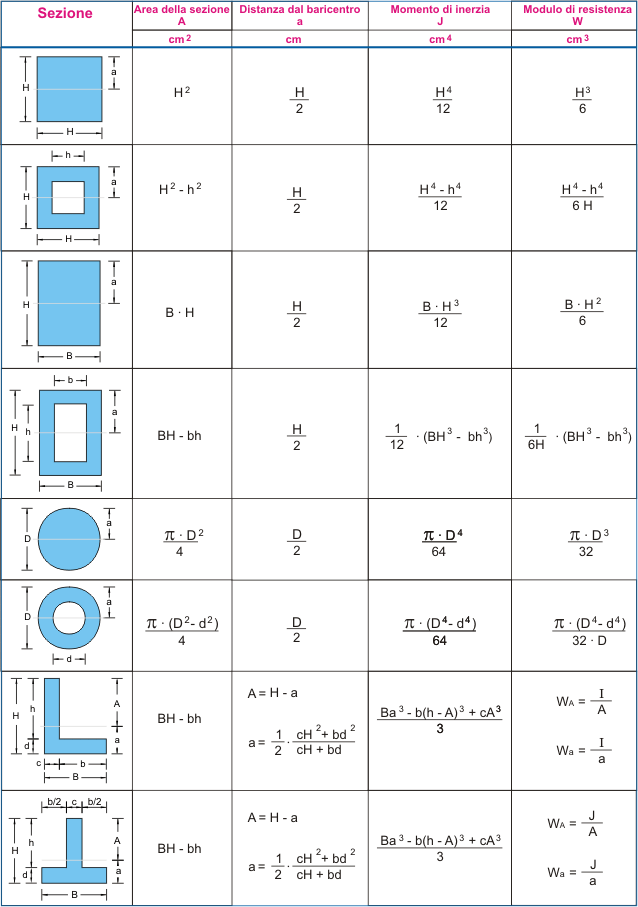
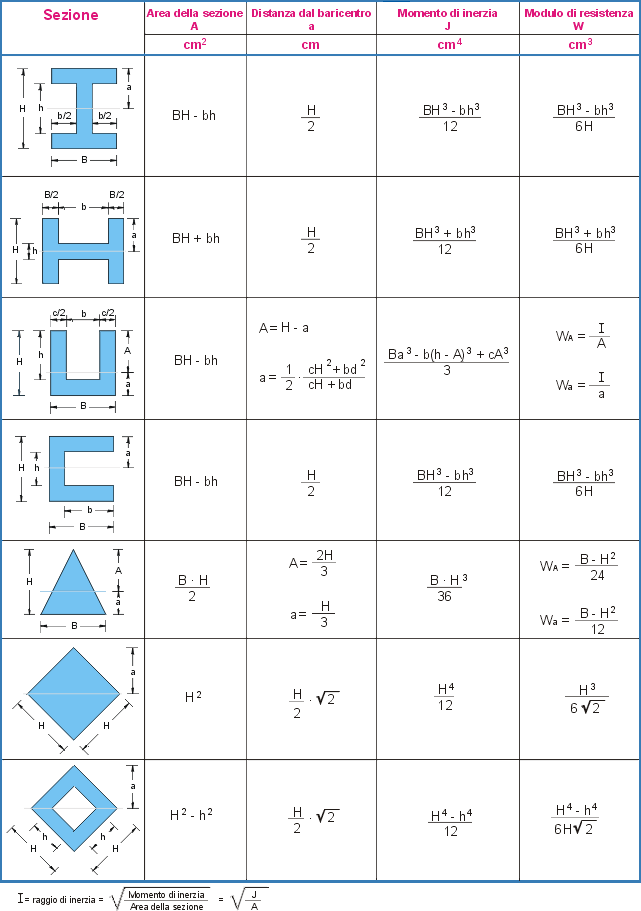
Il momento di inerzia di superficie delle figure piane rispetto a un asse è utilizzato frequentemente nell ingegneria civile e nell ingegneria meccanica.

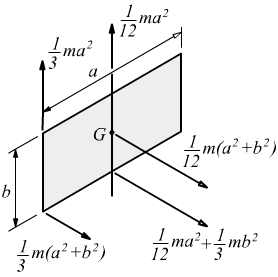
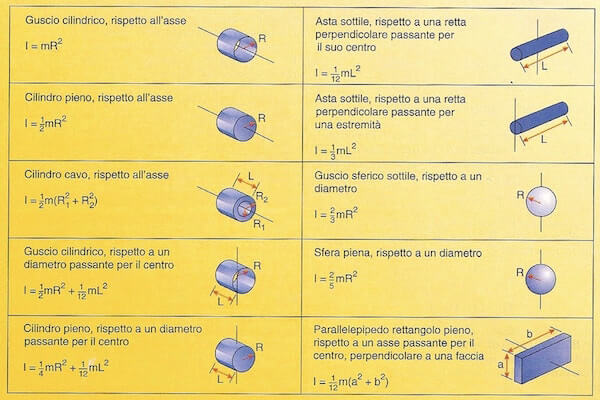
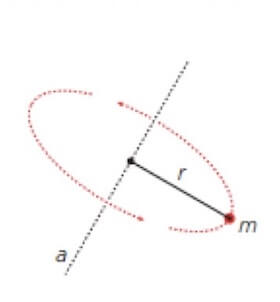
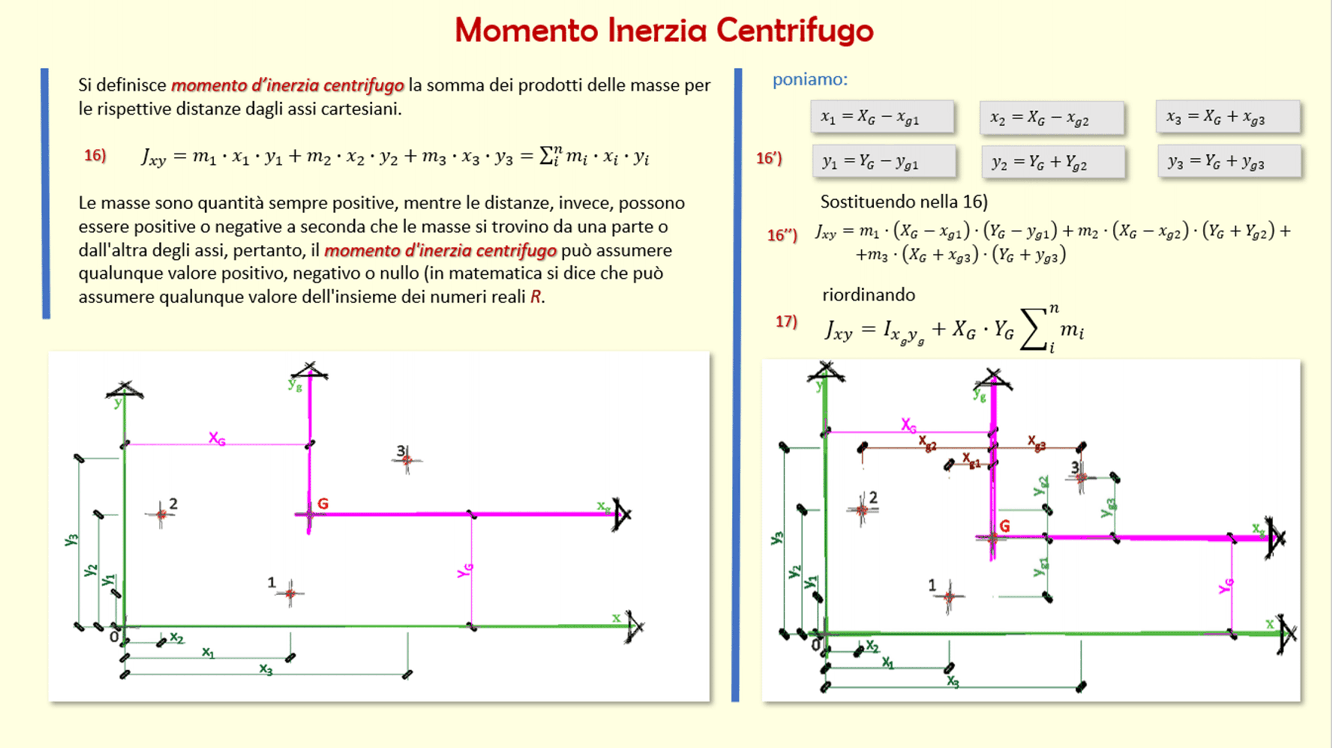
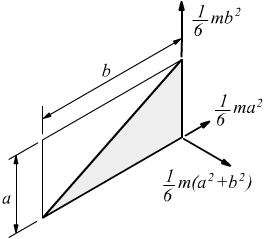
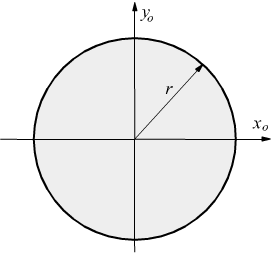
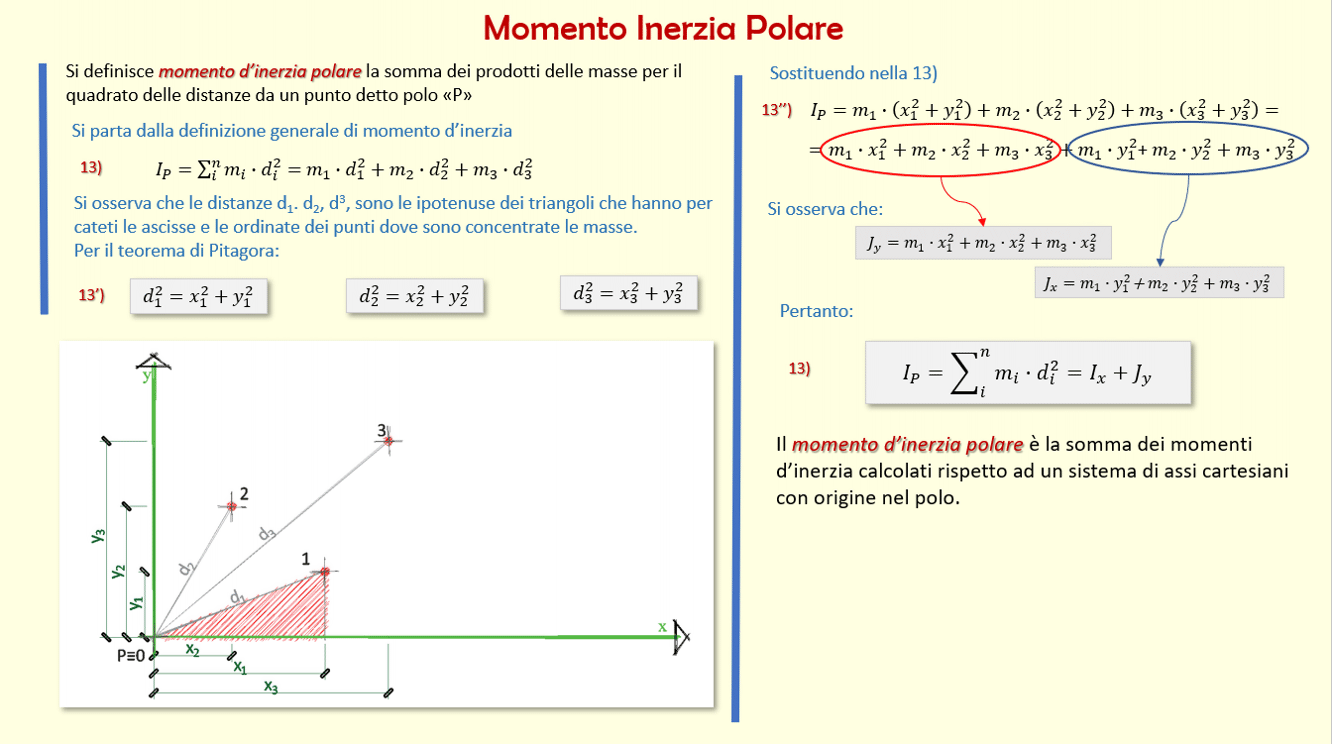
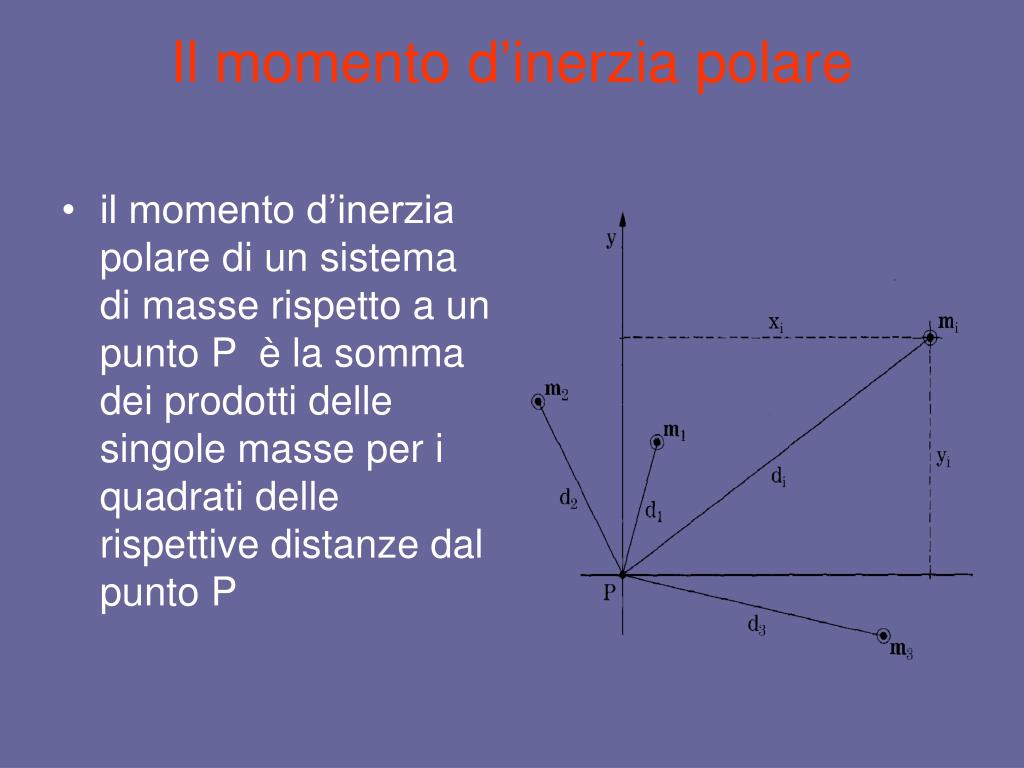
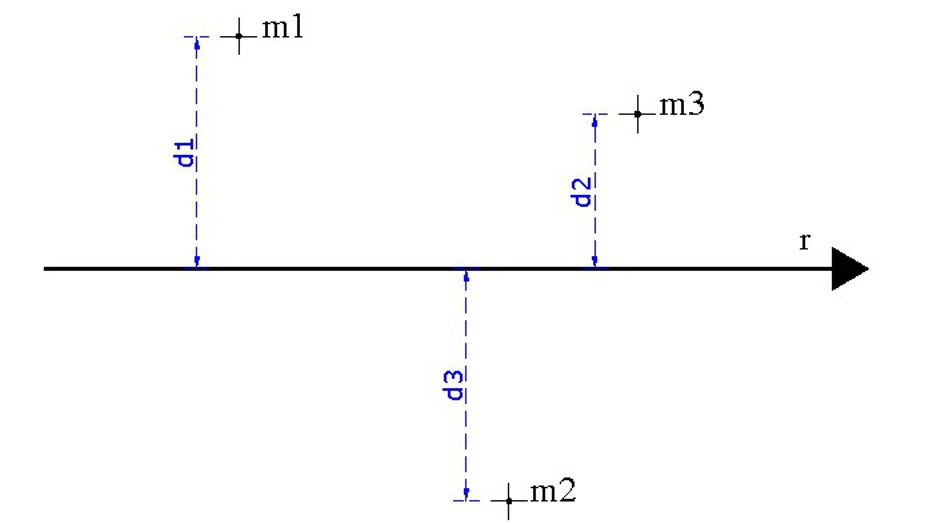
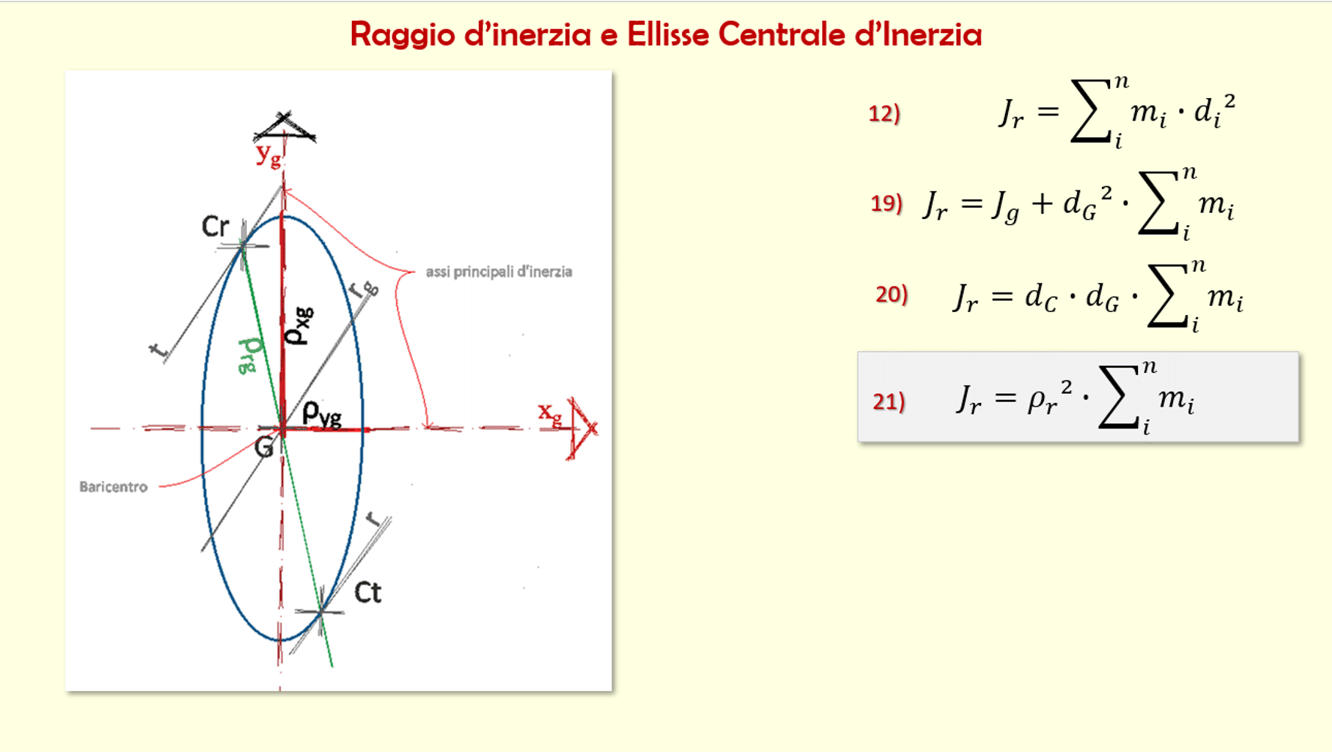
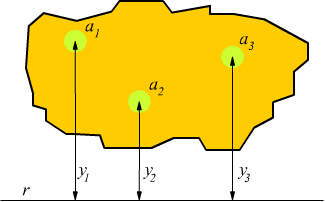
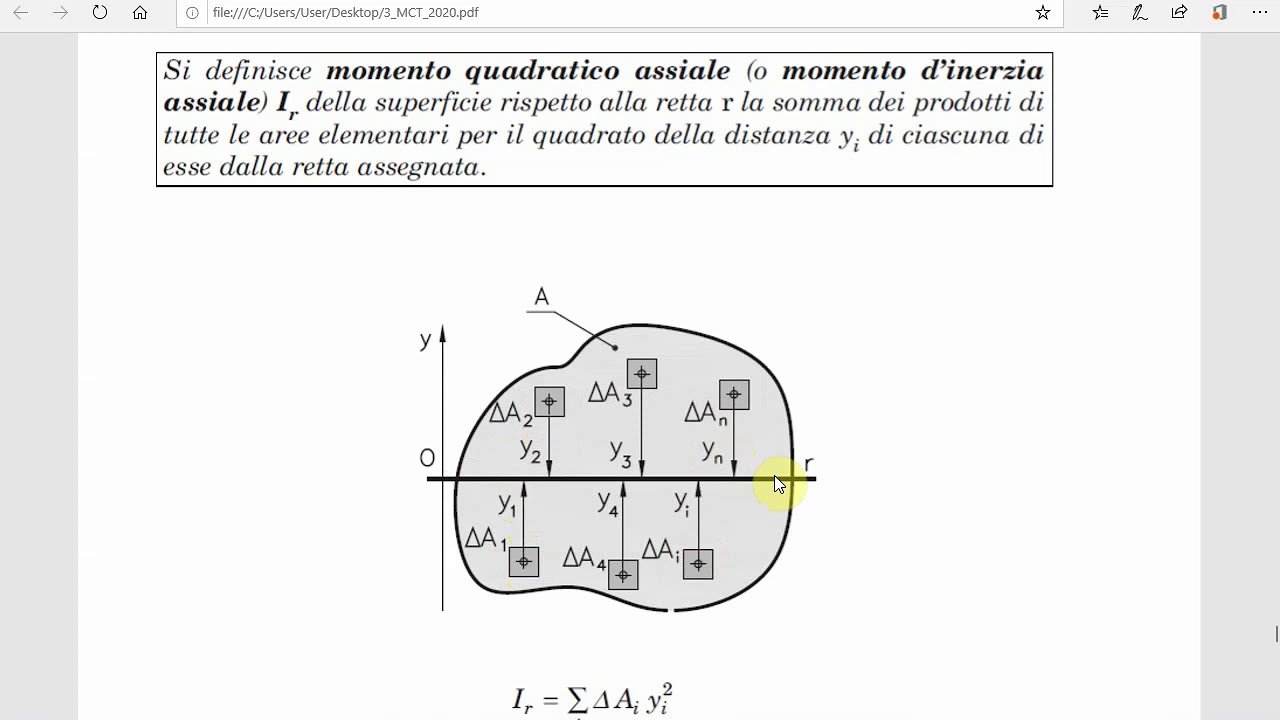
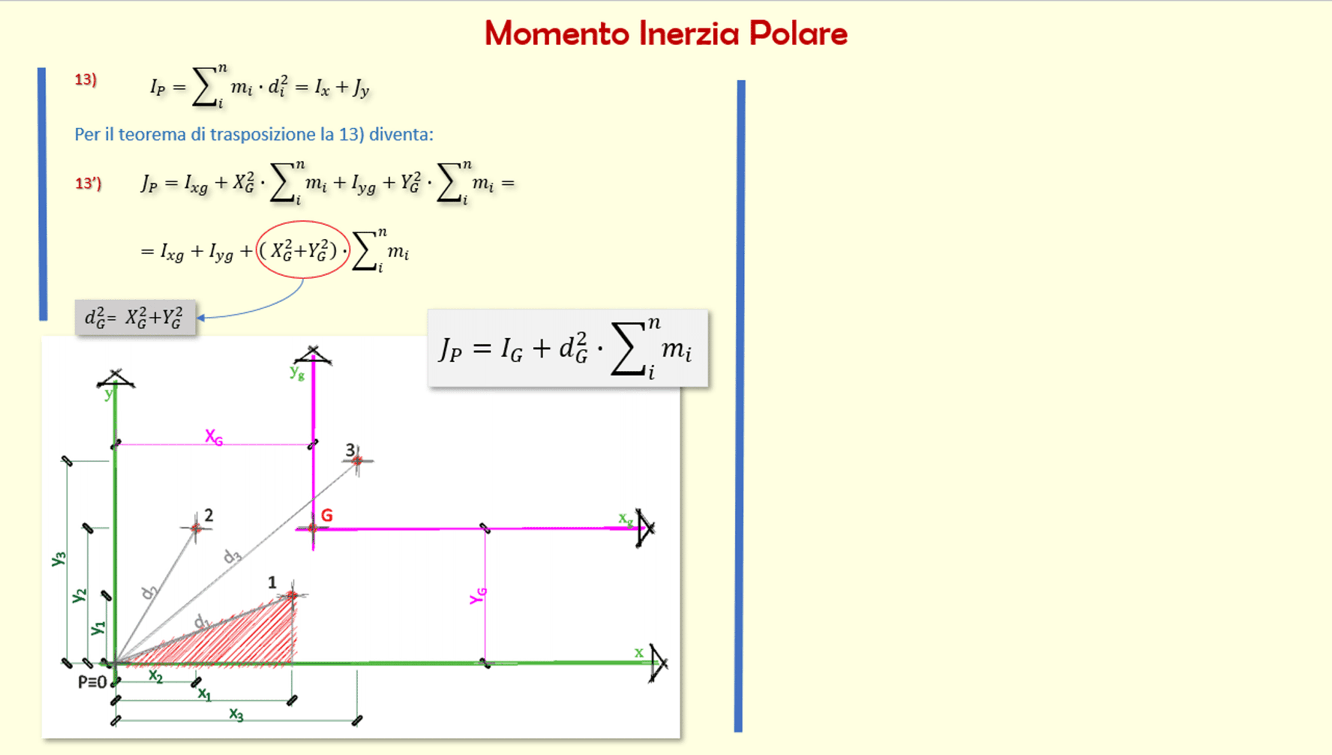
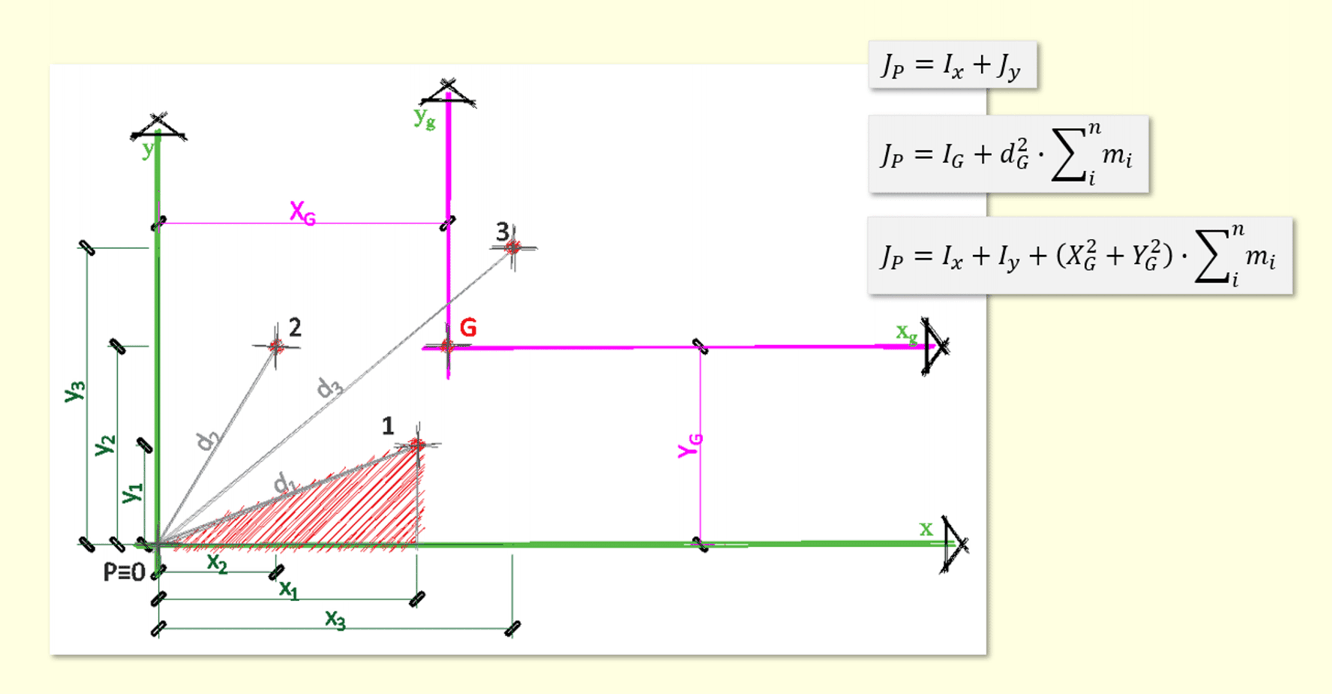
Momento di inerzia quadrato. Ii xx ad 2 0 dalla quale si ricava. Esso rappresenta la capacità del punto di opporsi al moto rotazionale. Una massa puntiforme non ha momento di inerzia intorno al proprio asse ma usando il teorema degli assi paralleli huygens steiner si ottiene un momento di inerzia intorno a un asse di rotazione distante. Momento polare di inerzia si definisce momento polare di inerzia di una superficie rispetto ad un punto p complanare alla superficie la sommatoria dei prodotti delle singole aree elementari a i per i quadrati delle rispettive distanze d i dal punto p.

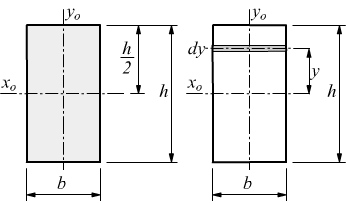
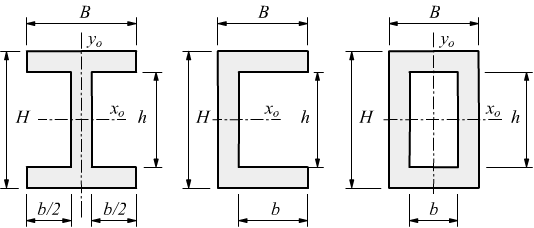
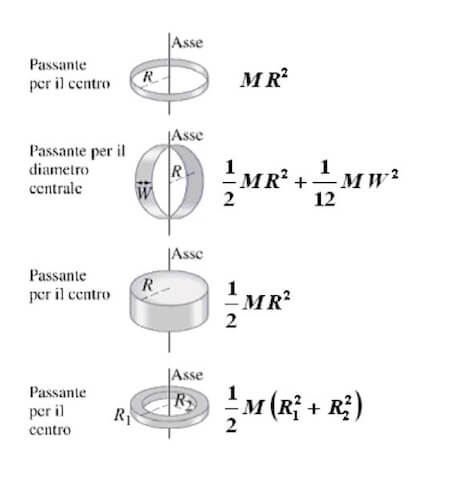
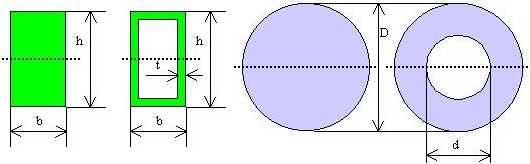
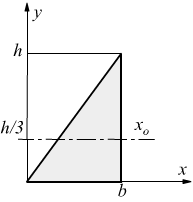
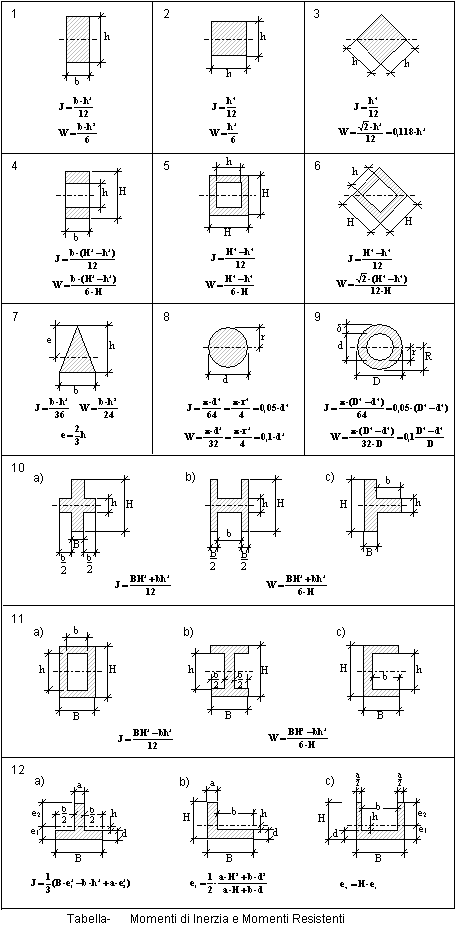
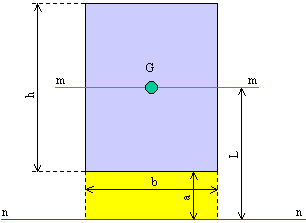
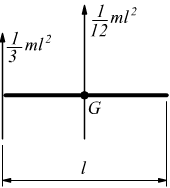
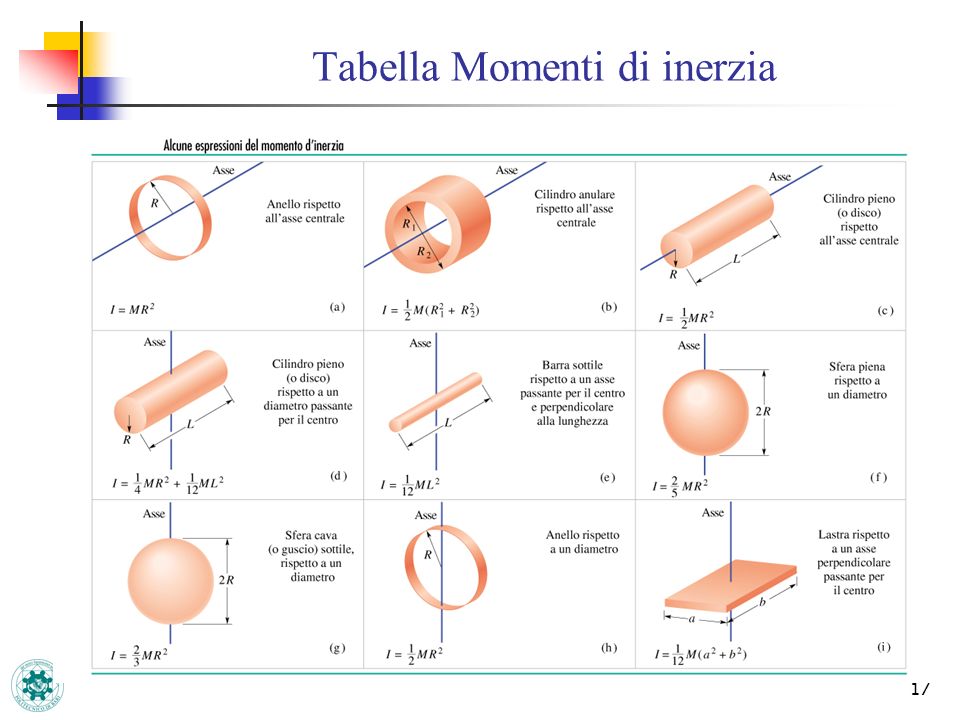
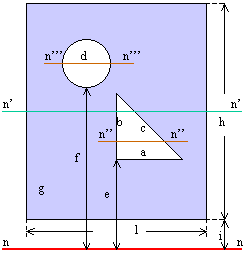
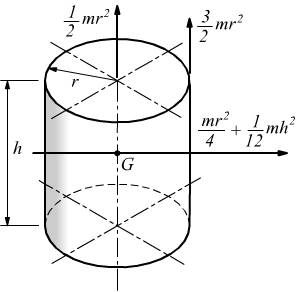
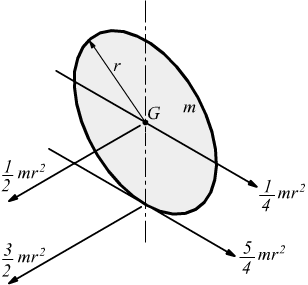
Tanto maggiore è il momento di inerzia tanto più è difficile far ruotare il punto attorno all asse scelto. H h 2 x 0 x 0 y i b h b h 2 4 momento d inerzia di un triangolo rispetto a un asse pas. Descrizione figura momento di inerzia commento massa puntiforme m a distanza r dall asse di rotazione. 1 il momento d inerzia è definito come il prodotto della massa per il quadrato della distanza del punto dall asse di rotazione.

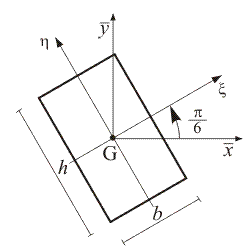
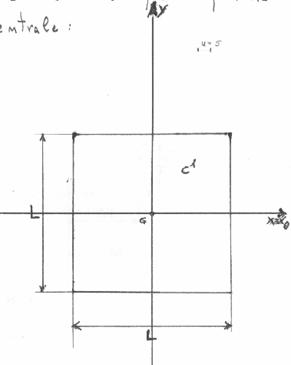
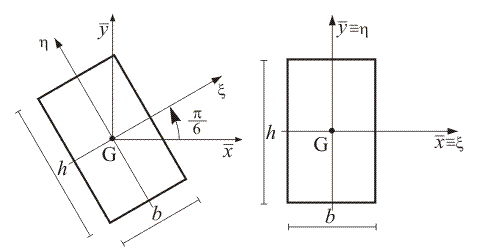
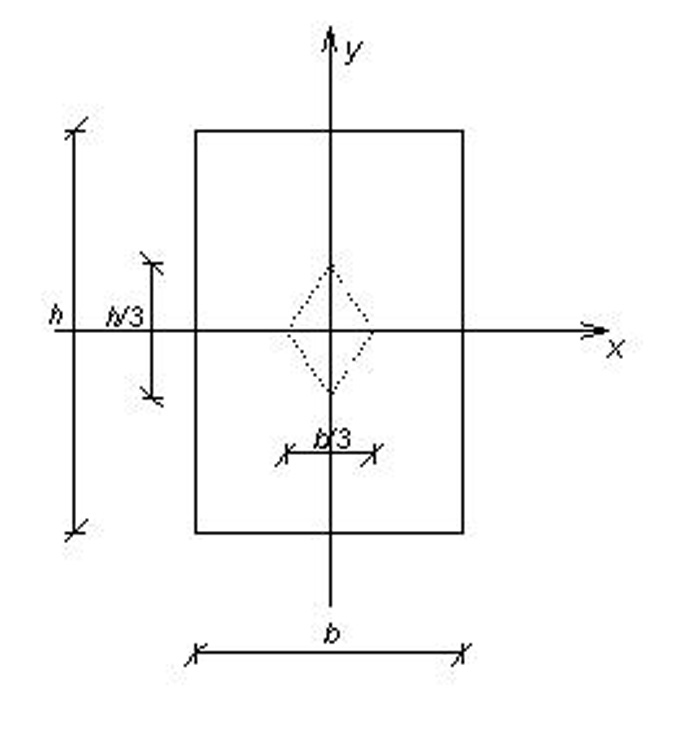
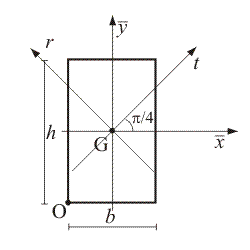
Il momento d inerzia rispetto ad un asse t si ottiene sommando al momento d inerzia rispetto all asse t 0baricentrico e parallelo a t il prodotto dell area a della superficie per il quadrato della distanza d2 fra le rette t e t 0. Infatti esso è direttamente correlato alla resistenza della sezione di un elemento soggetto a flessione rispetto ai carichi ortogonali all asse di riferimento. Determinazione del momento d inerzia di un quadrato rispetto alla sua diagonale. Per la ricerca del momento d inerzia rispetto all asse baricentrico x 0 ci si avvale ancora della formula di trasposizione.