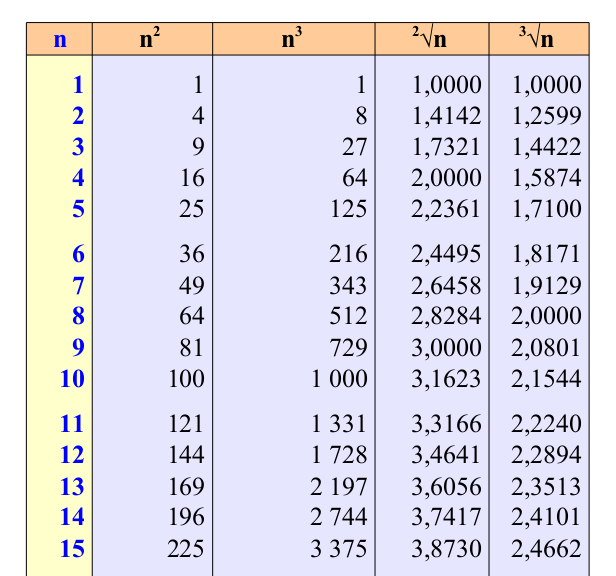
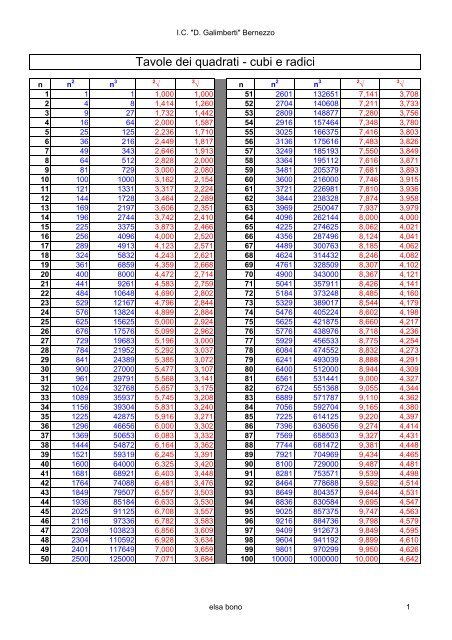
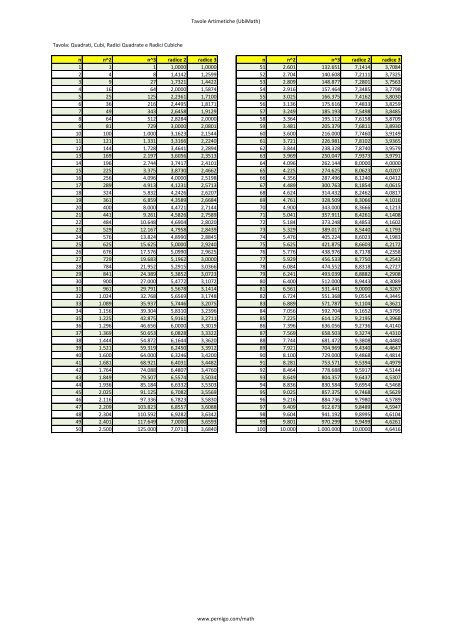
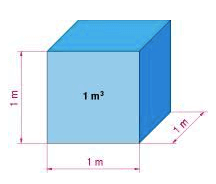
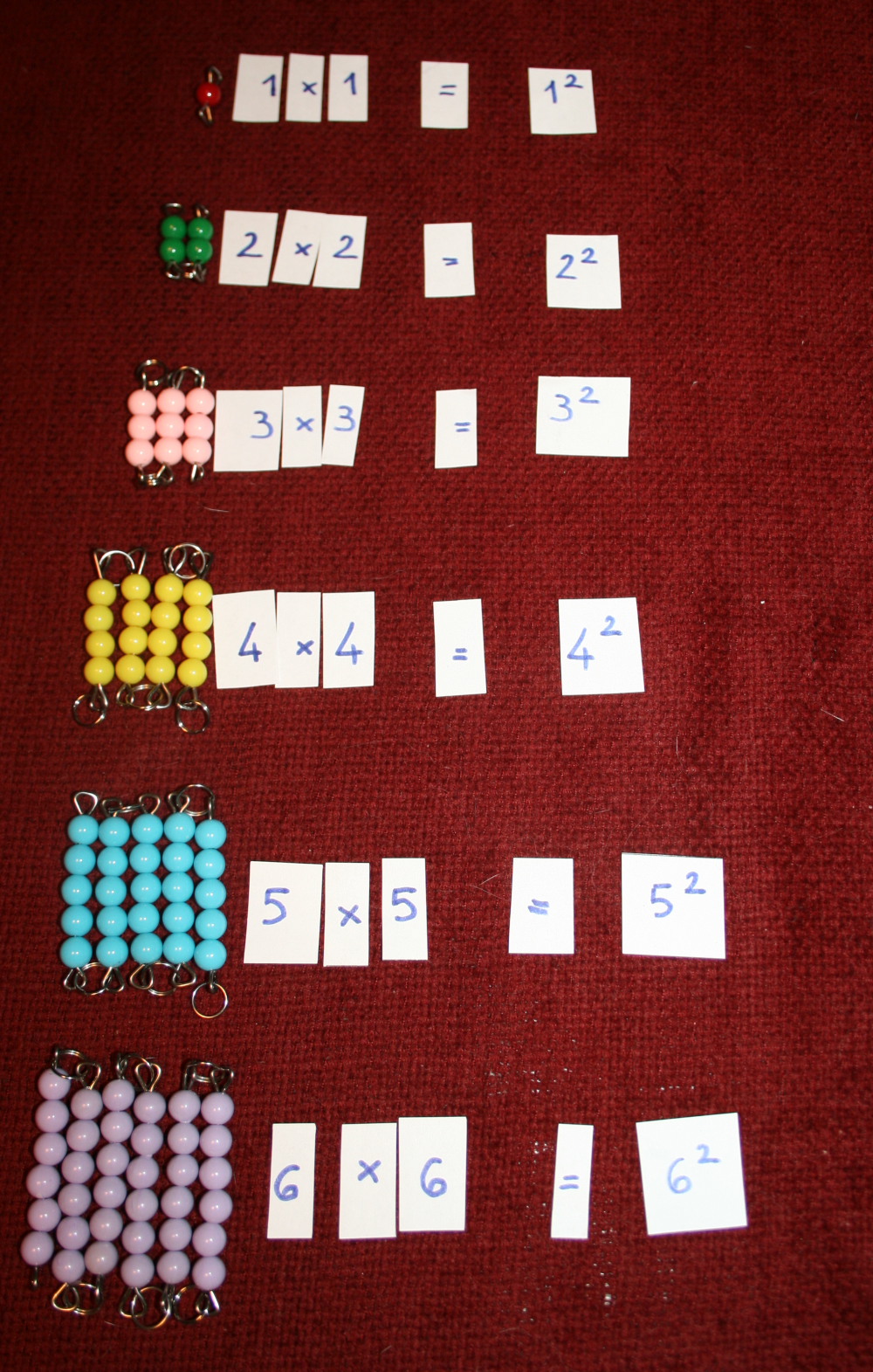
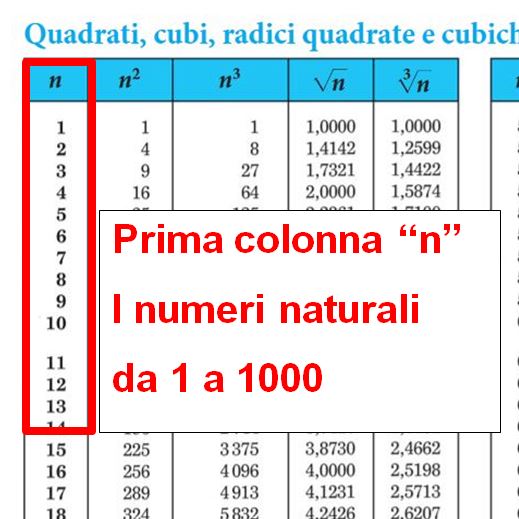
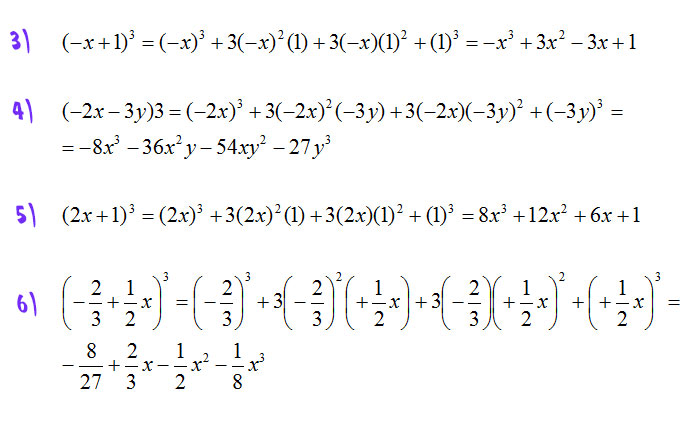Cubi E Quadrati

Effects of changes in y mx b.

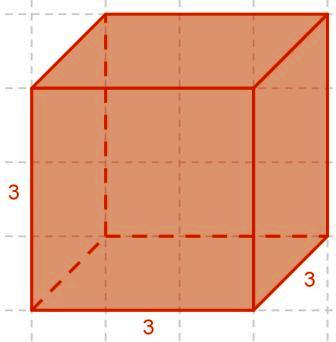
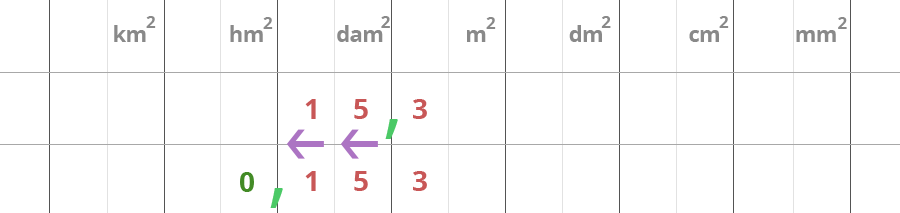
Cubi e quadrati. How to discover for yourself the solution of the cubic. A cubic polynomial in general will be of the form p left x right a x 3 b x 2 cx d a ne rm 0 once again the constraint that a should not be equal to 0 is required because if a is 0 then this becomes a quadratic rather than a cubic polynomial. Divide both sides of the equations by a. In this method we try to reduce the quadratic equation into a perfect square.

This page is intended to be read after two others. The steps for solving the equations are. Let us imagine ourselves faced with a cubic equation x 3 ax 2 bx c 0. If the quadratic equation is of the form a x 2 b x c 0.

The cubic equation has either one real root or it may have three real roots. The quadratic equation is thus written as x 2 sum of the root x product of the roots 0. 2 x 3 3 x 2 6 x 9 0 x 3 9 x 1 0 x 3 1 5 x 2 0. The solutions of this equation are called roots of the cubic function defined by the left hand side of the equation.

Linear quadratic and cubic models used to describe physical items or situations. Method of perfect square. B y intercept if m 0 then line is horizontal y b if m undefined then line is vertical run 0 not a function if m 0 the slope is positive line increases from left to right the larger the slope the steeper the line if m 0 the slope is negative line decreases from left to right. To solve this equation means to write down a formula for its roots where the formula should be.

In algebra a cubic equation in one variable is an equation of the form in which a is nonzero. If all of the coefficients a b c and d of the cubic equation are real numbers then it has at least one real root this is true for all odd degree polynomial functions. Is z 2 frac z 6 z 7 z 4 4 a cubic polynomial. This may be easy to solve quadratic equations with the help of quadratic formulas but to make them useful in daily application you must have a depth understanding of the program.

This means the following are all cubic equations.