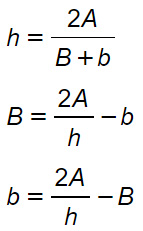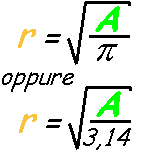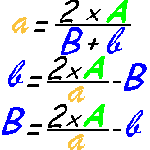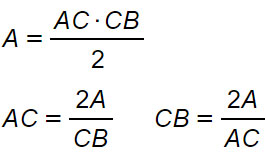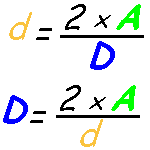Area Quadrato Formule Inverse

In geometria il rettangolo è un quadrilatero che ha tutti gli angoli interni congruenti tra loro e di conseguenza retti. Nel caso in cui il problema dovesse fornirci la misura della diagonale del quadrato possiamo ricavare la misura del lato con la formula inversa e poi elevare il risultato al quadrato. Quadrato formule inverse marzo 2 2016 webinfo in geometria il quadrato è un quadrilatero regolare cioè un poligono con quattro lati congruenti e quattro angoli uguali tutti retti.

moneta con buco quadrato msi ws65 quadro rtx moma new york quadri famosi mostra fendi roma colosseo quadrato monete quadrate momenti quadri mostra quadri mostre quadri 2020

Area Del Rettangolo E Del Quadrato

Facebook

Il Formulario Del Perimetro Professionisti Scuola

Didattica Matematica Scuola Primaria Dall Area Alla Misura Dei Lati Classe Quinta

Poligoni Equivalenti Proprieta Riflessiva A A Proprieta Simmetrica Ppt Scaricare

Perimetro Del Quadrato E Del Rettangolo

Oppure si utilizza una formula diretta.

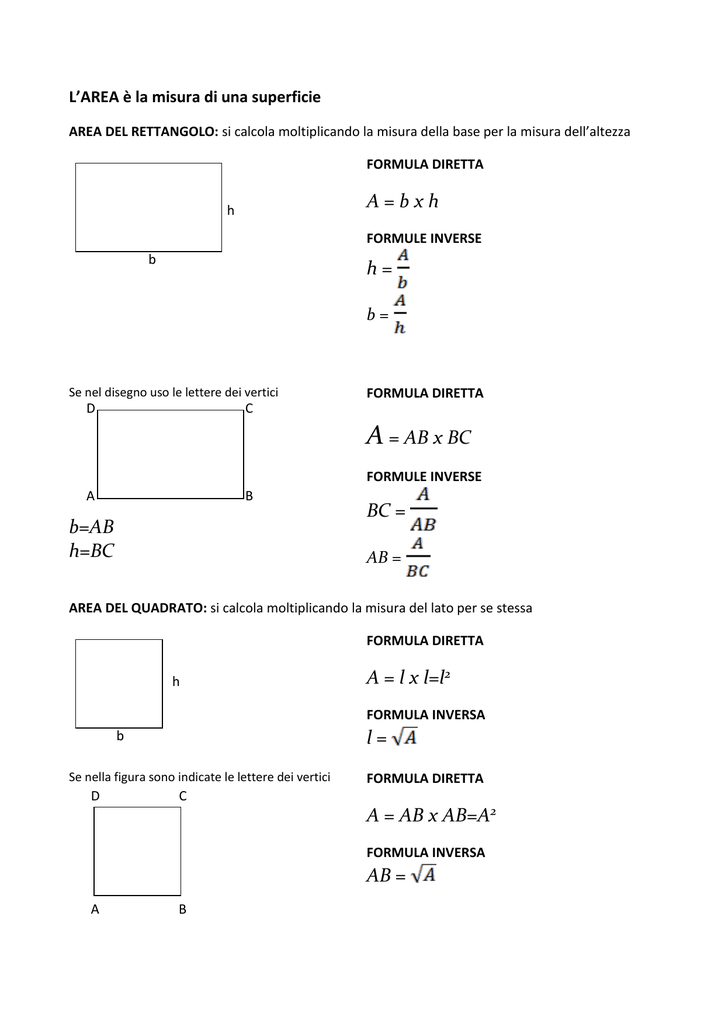
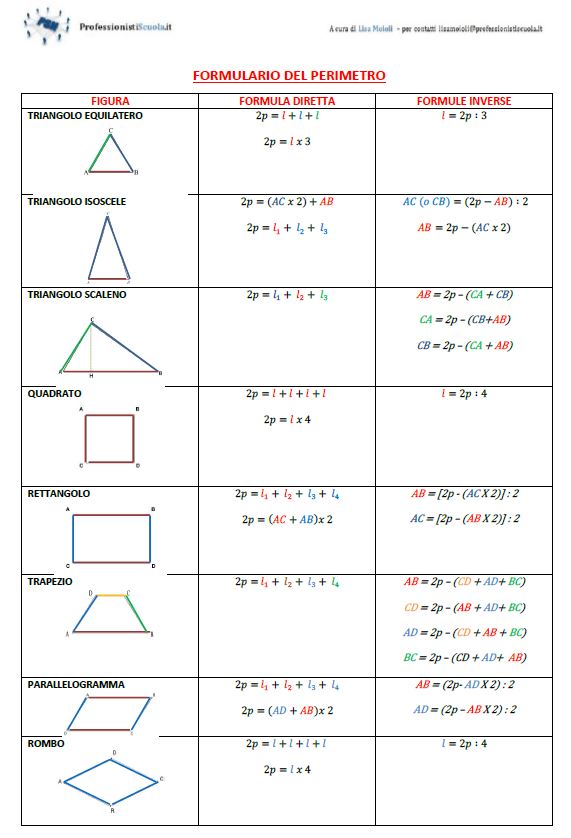
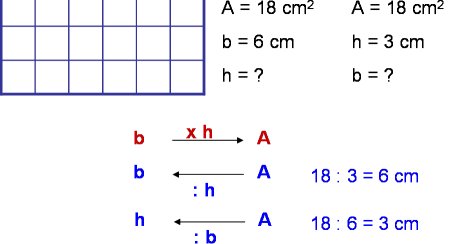
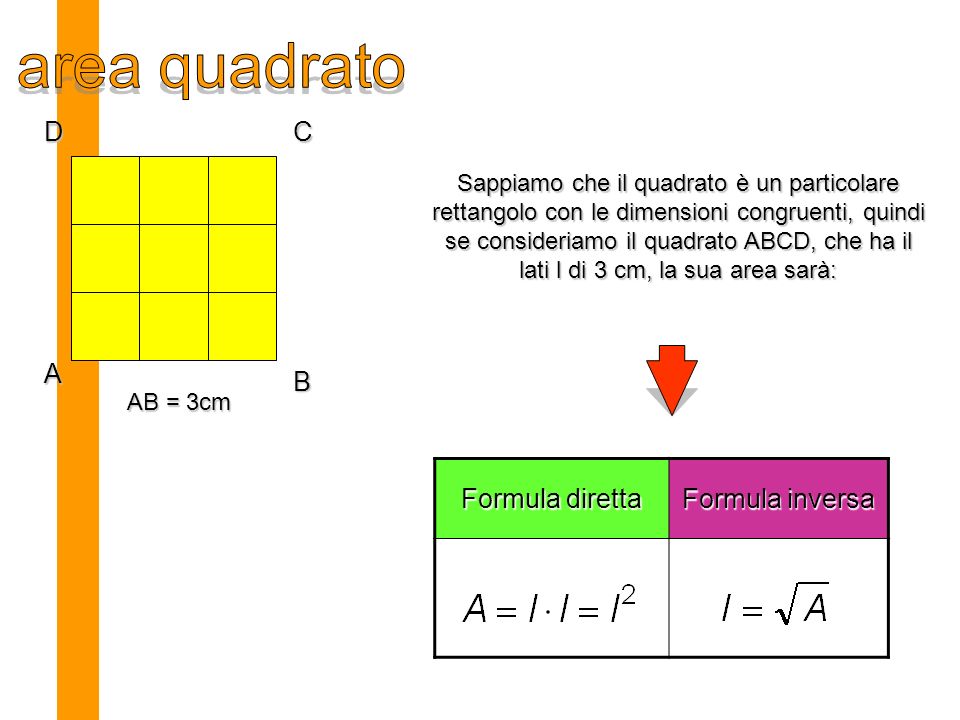
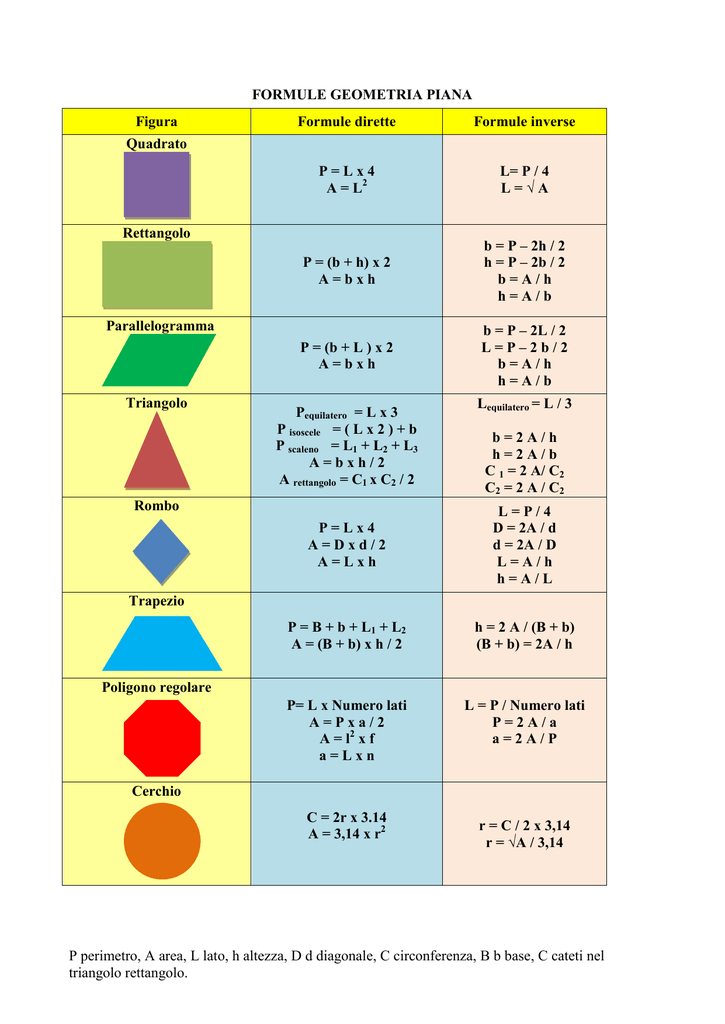
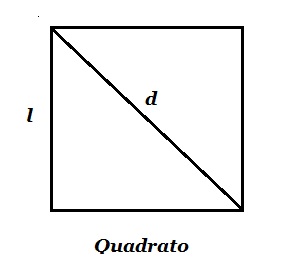
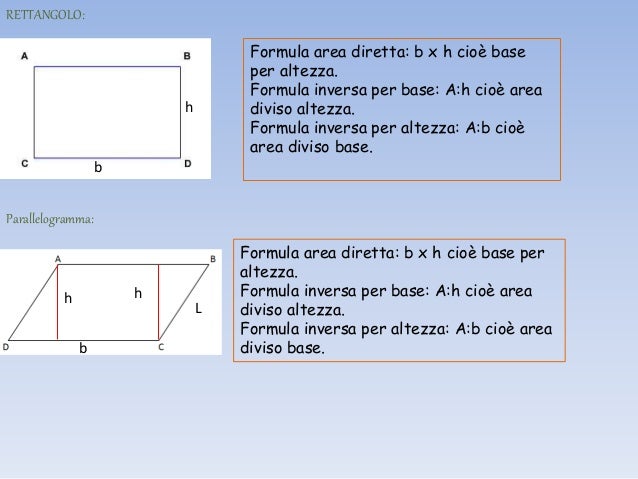
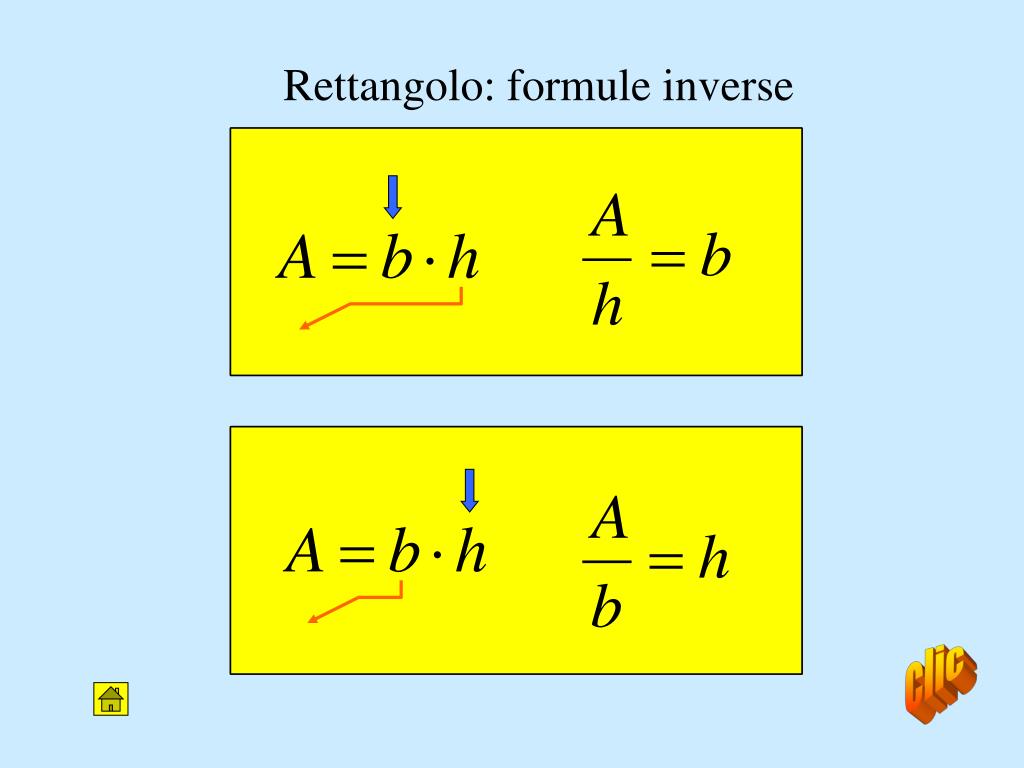
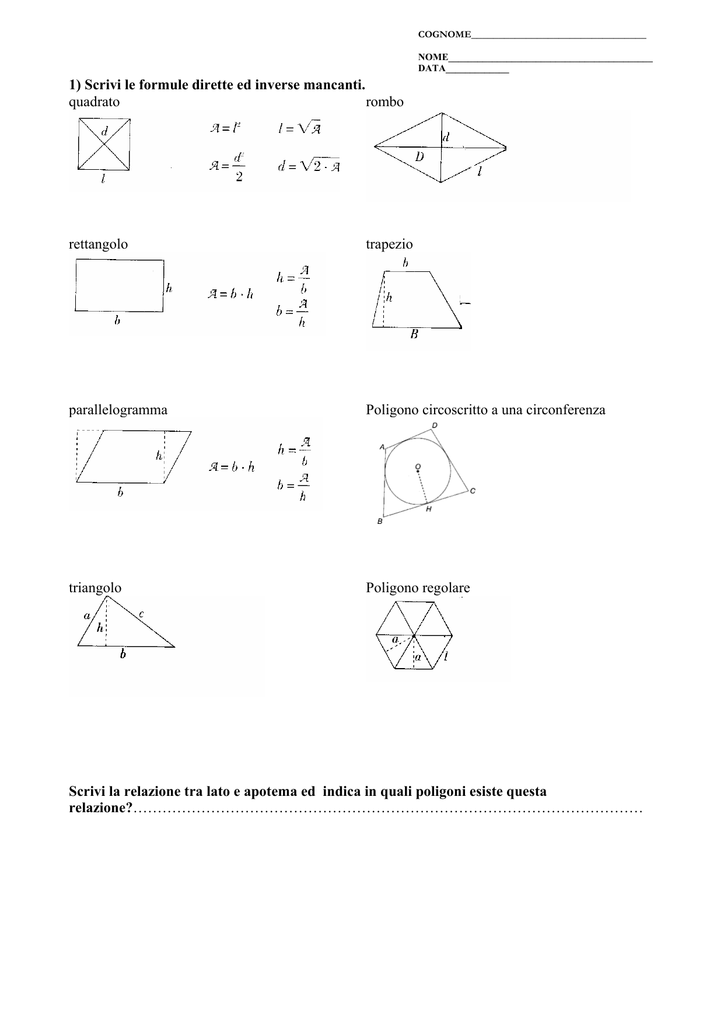
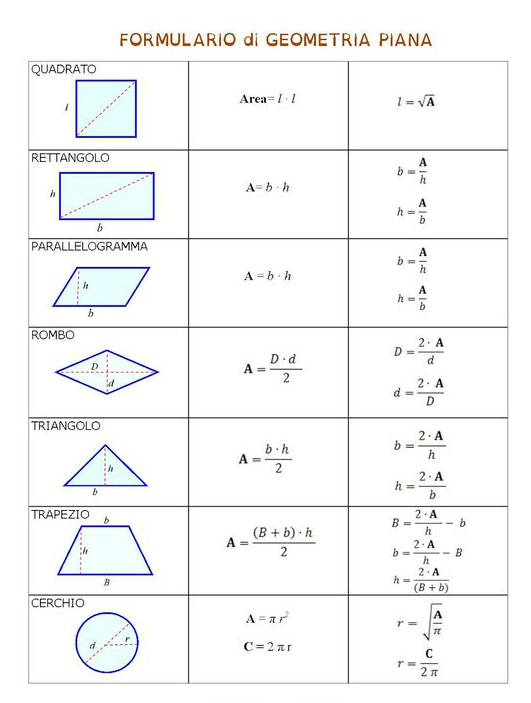
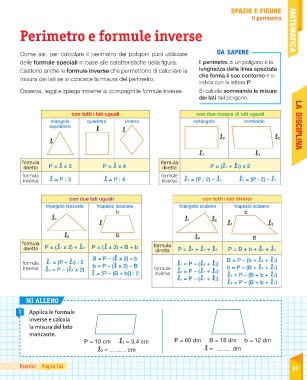
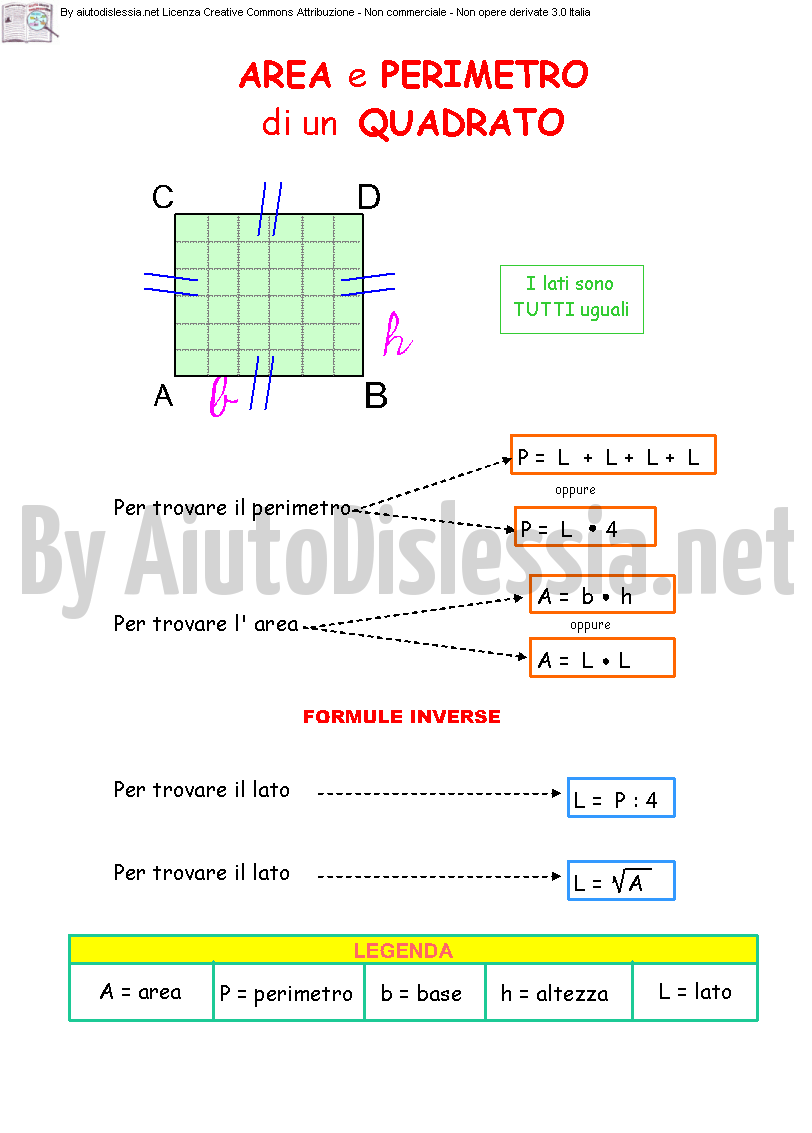
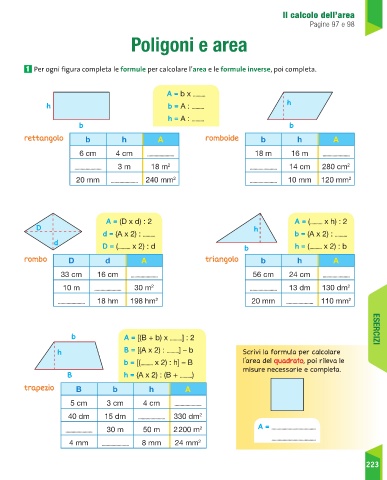
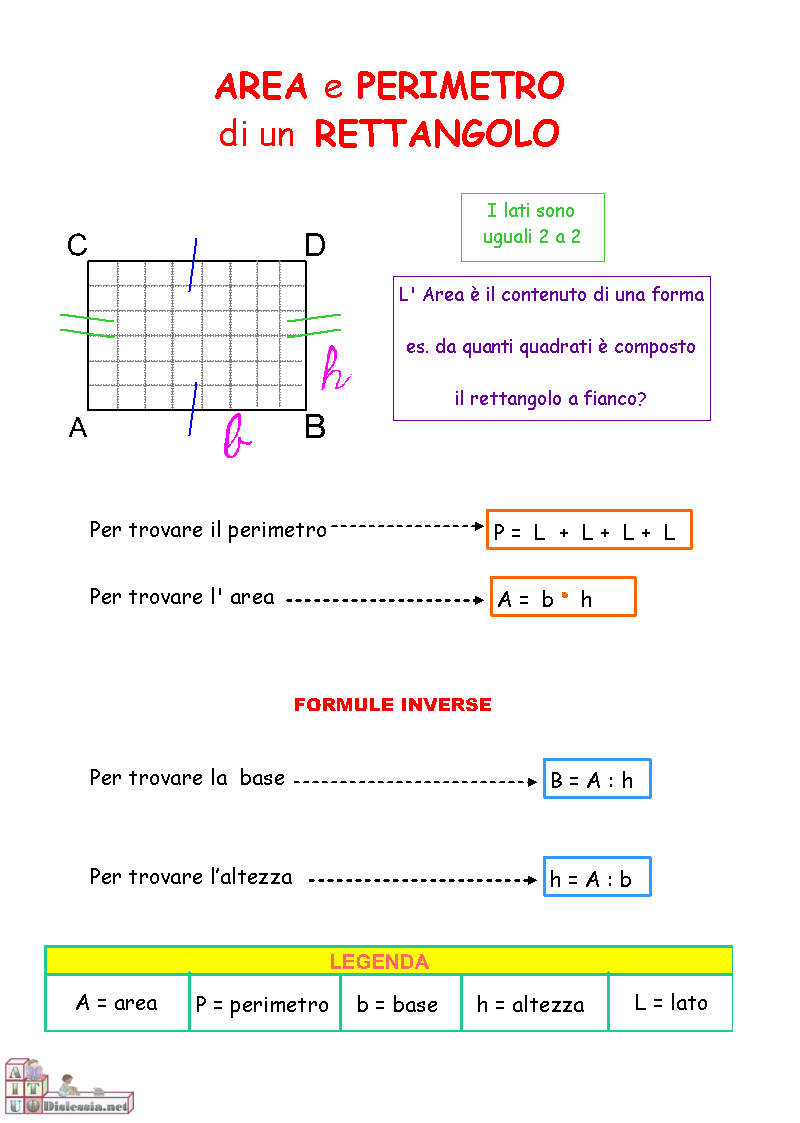
Area quadrato formule inverse. B a h 24 4 cm 6. Indichiamo con l il lato del quadrato con d la diagonale del quadrato con 2p il perimetro e con a l area. Da questa definizione si evince che in un rettangolo ciascuna delle due coppie di lati opposti è costituita da lati congruenti. Sappiamo anche che l operazione inversa all elevamento al quadrato è l estrazione della radice quadrata.

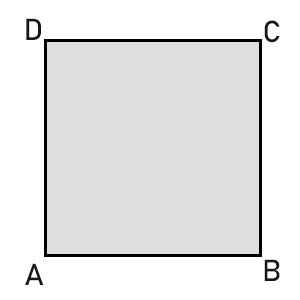
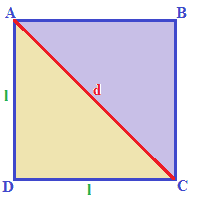
La formula inversa conoscendo il lato è. Quindi nel nostro esempio per trovare il lato del quadrato dovremo fare. Perimetro del quadrato conoscendo la diagonale. Quadrato formule inverse in geometria il quadrato è un quadrilatero regolare cioè un poligono con quattro lati congruenti e quattro angoli uguali tutti retti.

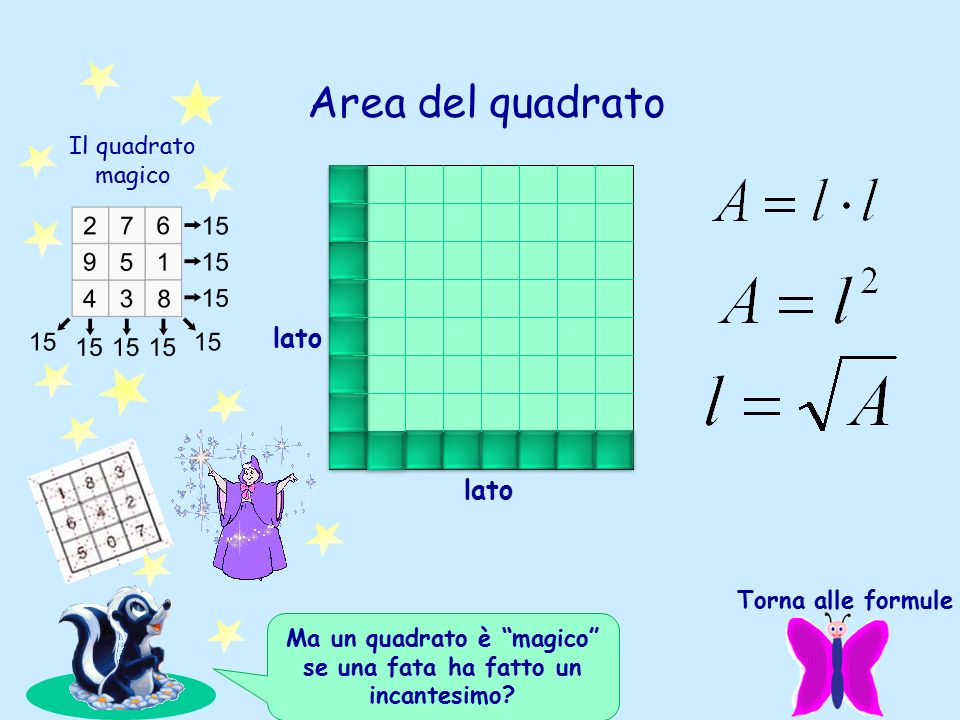
Lato del quadrato conoscendo l area. Per le formule inverse dell area del quadrato e per leggere tutte le proprietà del quadrato rimandiamo alla lezione del link. Perimetro del quadrato conoscendo l area. Come detto in precedenza le diagonali del quadrato sono due sono perpendicolari e formano due triangoli equilateri.

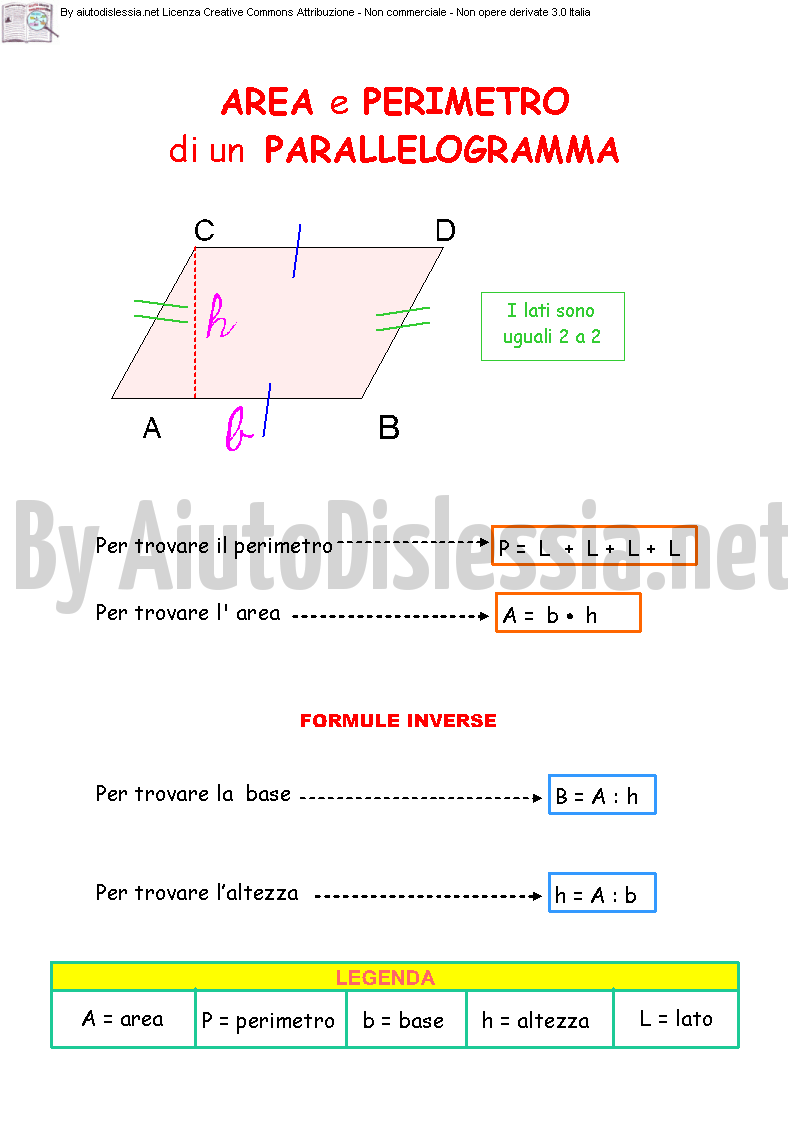
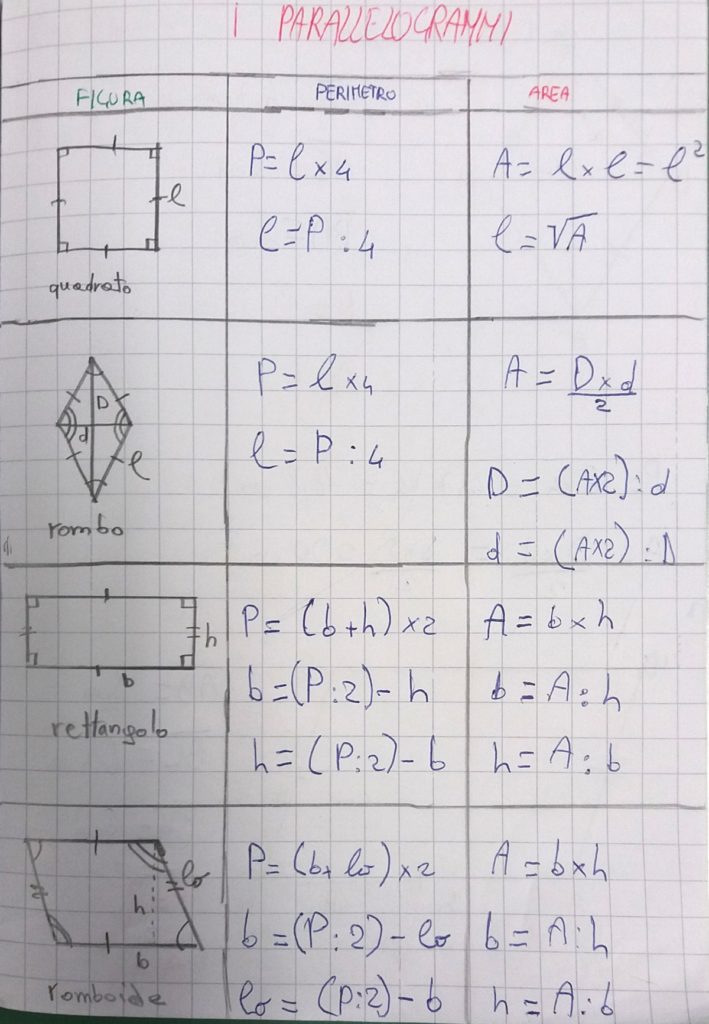
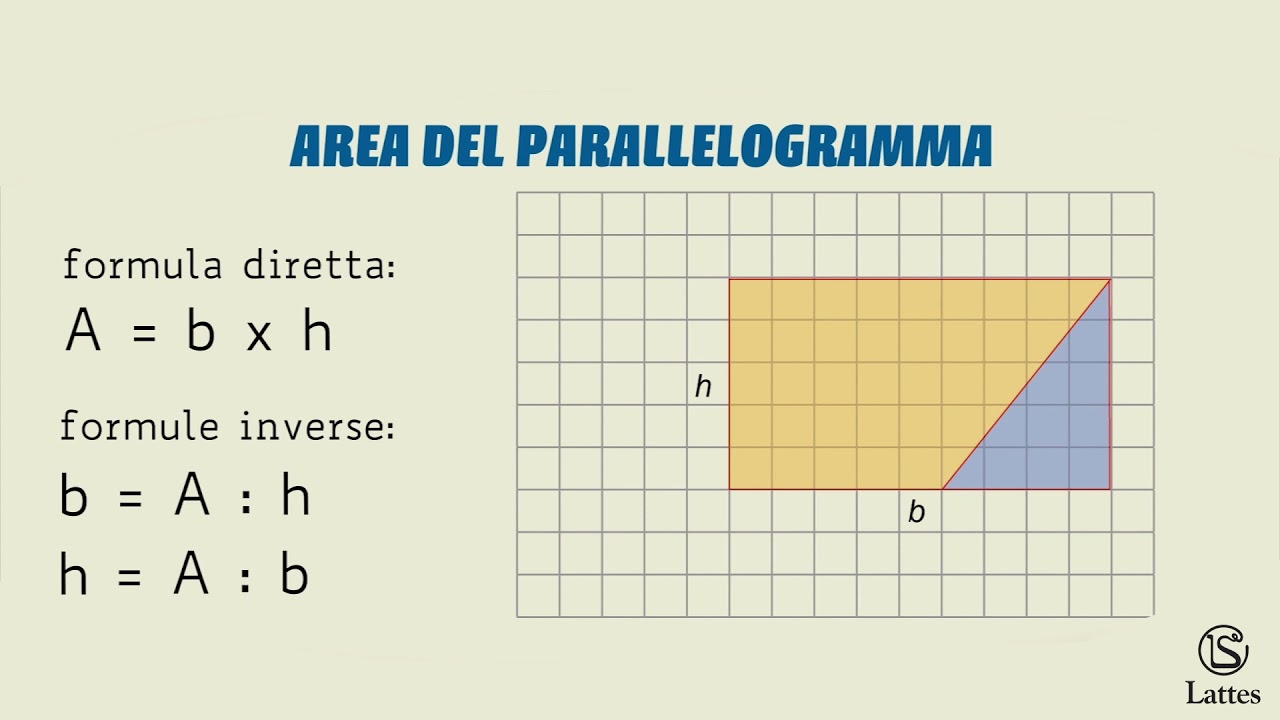
P l x 4. In altre parole i rettangoli sono particolari parallelogrammi. Per calcolare l area di un quadrato basta conoscere la misura del lato del quadrato che può essere ricavata sia dal perimetro che dalla misura della diagonale. La formula diretta per calcolare il perimetro è molto elementare.

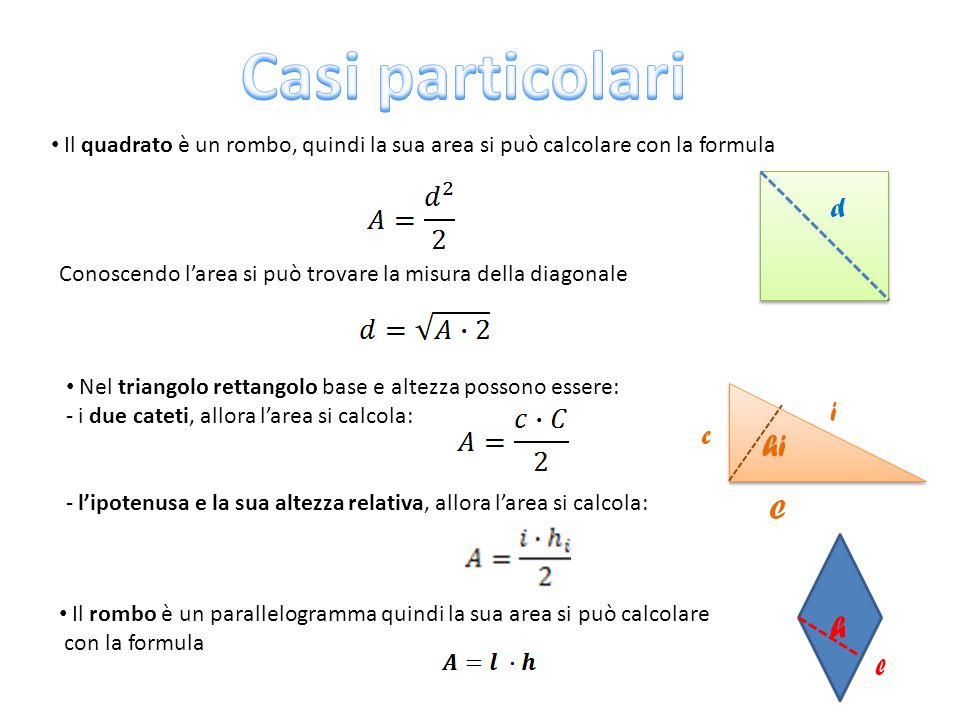
Perimetro del quadrato conoscendo il lato. Il quadrato è un caso particolare di rombo in quanto ha tutti e quattro i lati uguali e di rettangolo in quanto ha quattro angoli uguali quindi è un caso particolare di. Lato del quadrato conoscendo il perimetro. Calcolare l area del quadrato data la diagonale.

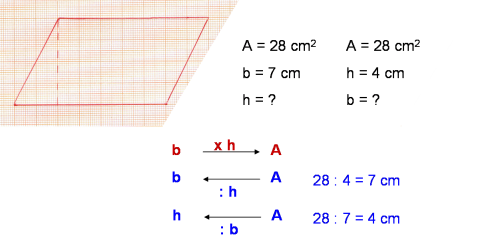
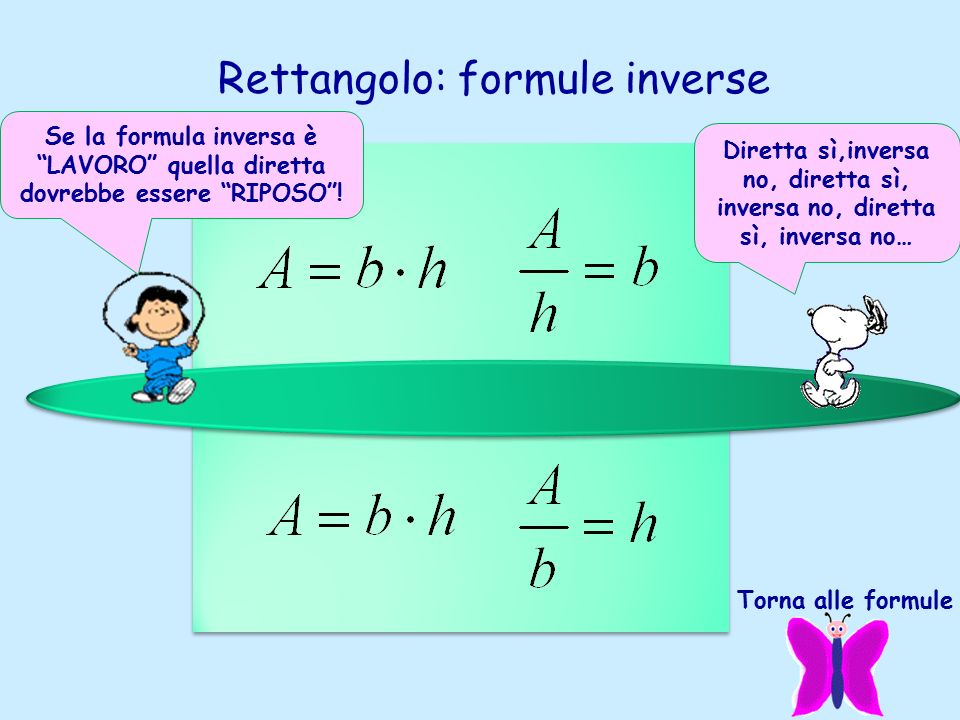
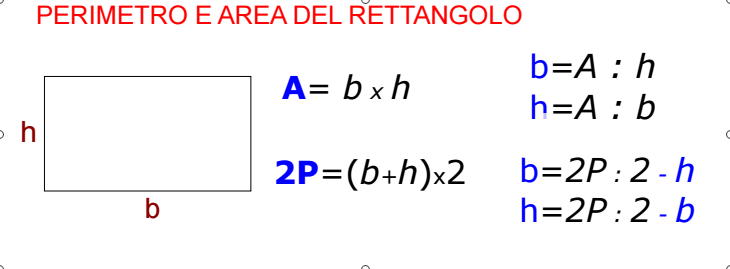
A area del quadrato. Da qui si possono ricavare diverse formule. Quindi ricapitolando la formula inversa è. H a b b a h.

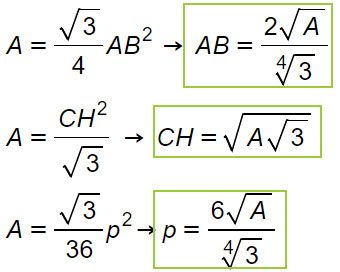
Per elencare le formule del quadrato partiamo dai nomi. L d 2. P a x 4. Quindi ricapitolando le formule inverse sono.

L p 4. Lato del quadrato conoscendo la diagonale. P d 2 x 4. In grassetto le formule da cui è possibile ricavare facilmente le formule inverse.