Apotema Quadrato

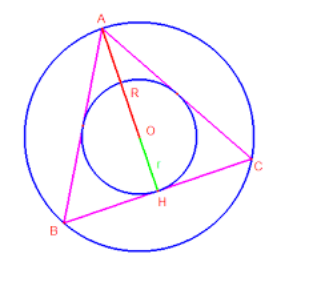
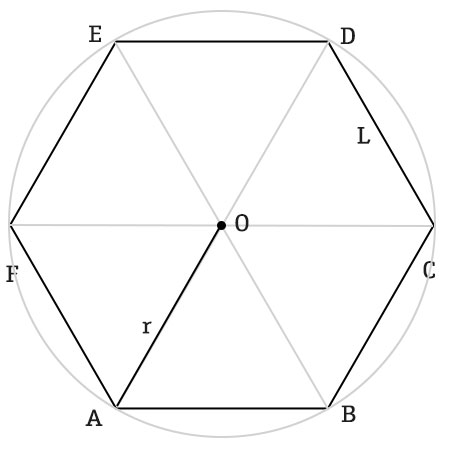
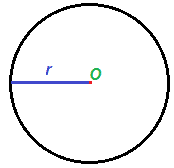
R raggio della circonferenza inscritta.

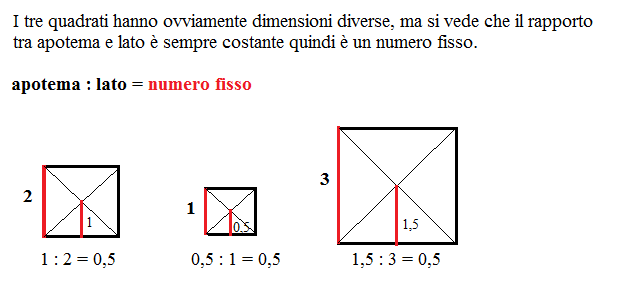
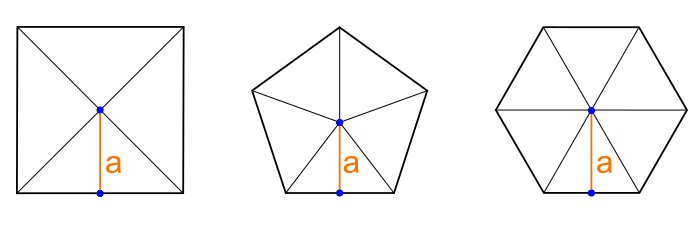
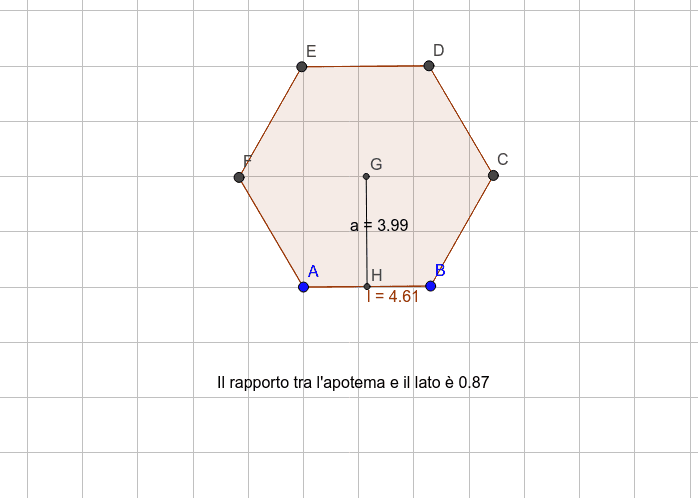
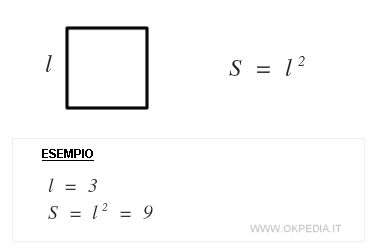
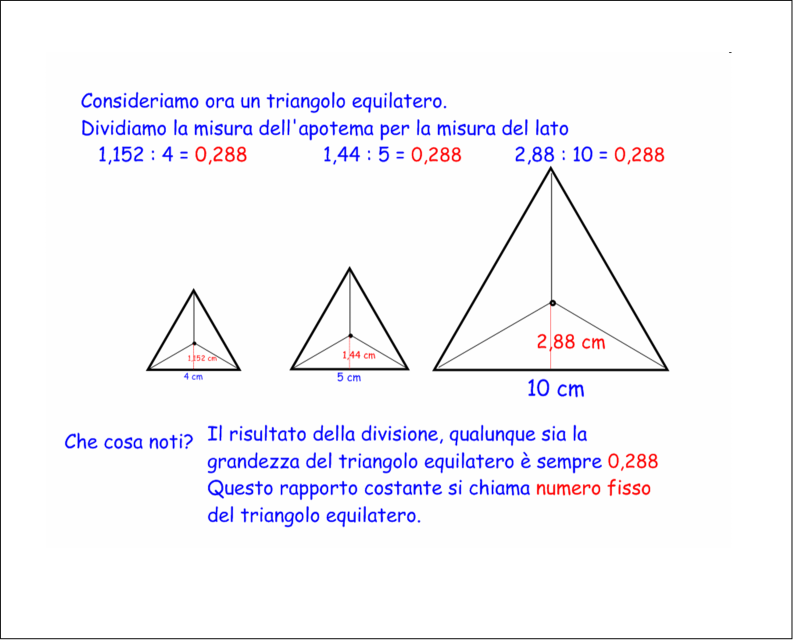
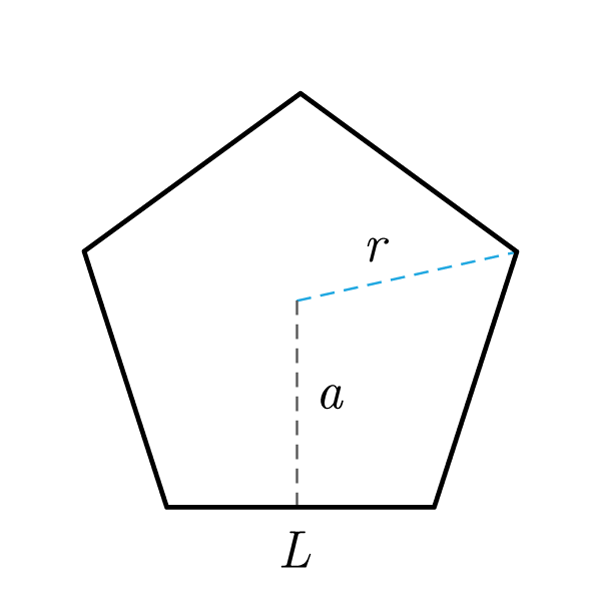
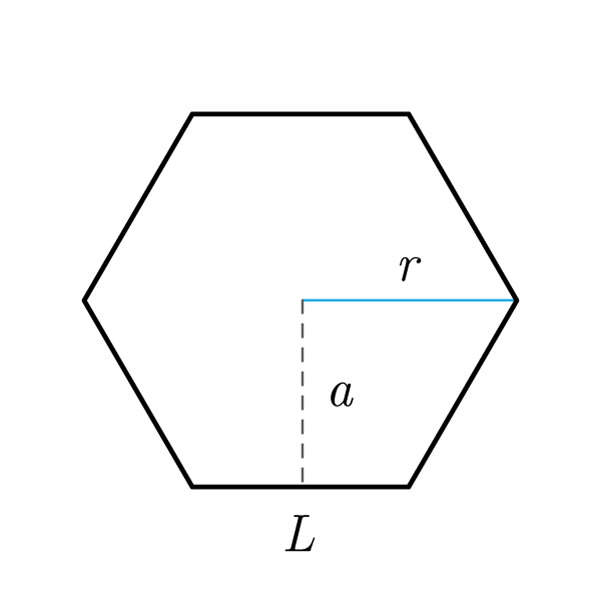
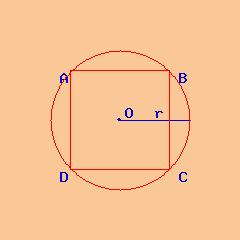
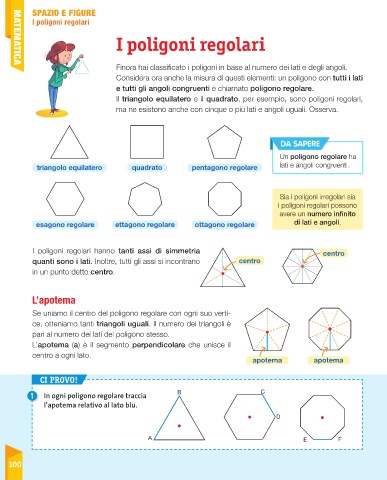
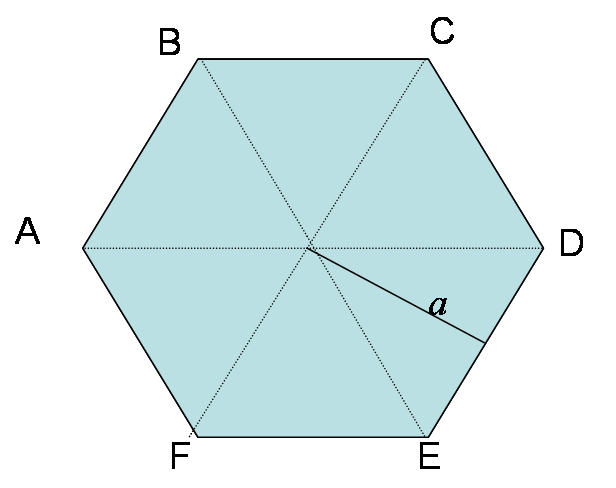
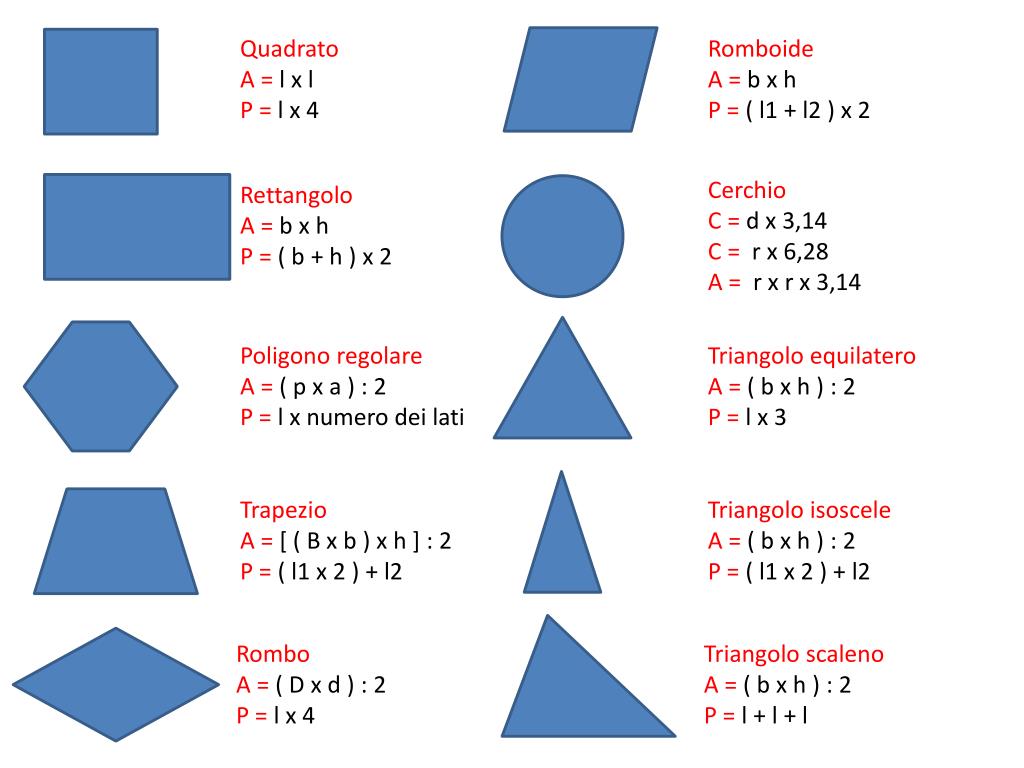
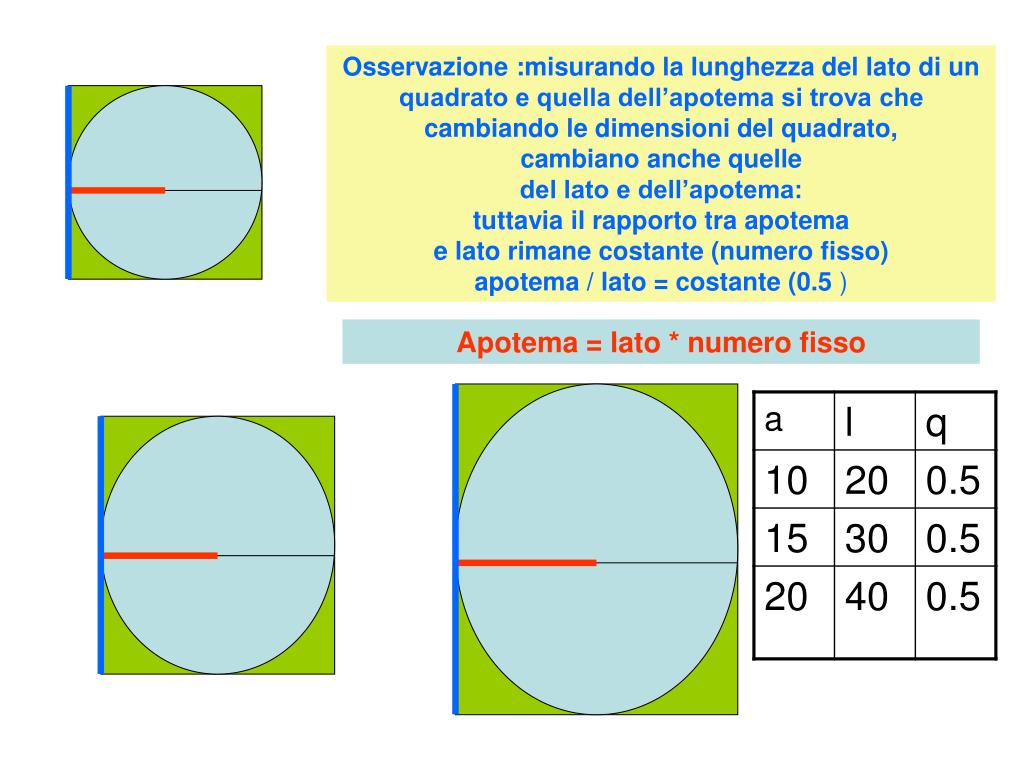
Apotema quadrato. Apotema lato x f se avrete un quadrato di lato 12cm vi basterà. Prendiamo ad esempio un quadrato un pentagono regolare ed un esagono regolare e disegniamo per ciascuno di essi la circonferenza inscritta ossia la circonferenza che ha come centro il centro del poligono e come raggio la distanza del centro dal lato del poligono. Dato un qualsiasi poligono regolare si dice apotema il raggio della circonferenza ad esso inscritta. In un poligono regolare se dividiamo l apotema per un lato otteniamo un numero detto numero fisso.

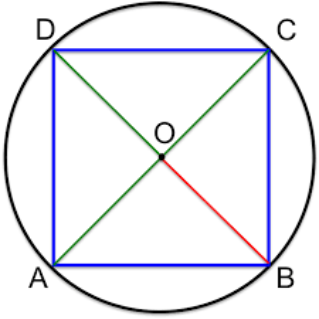
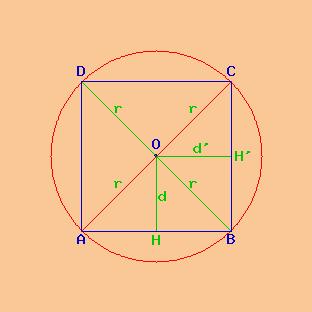
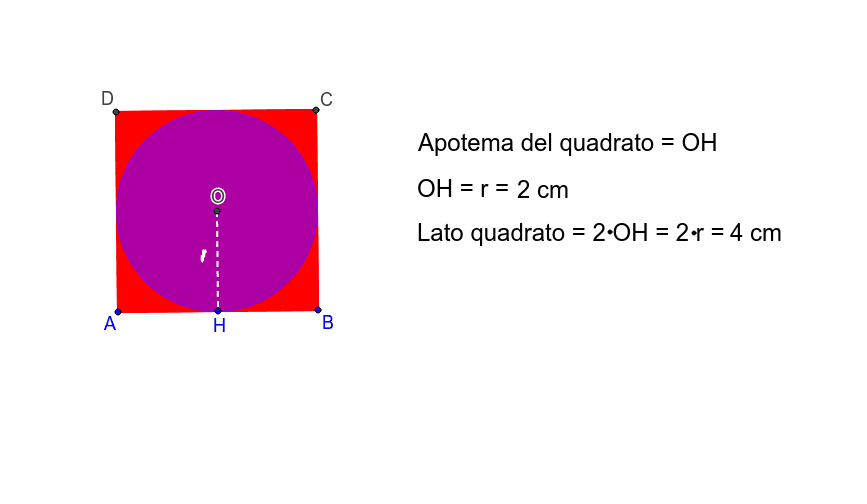
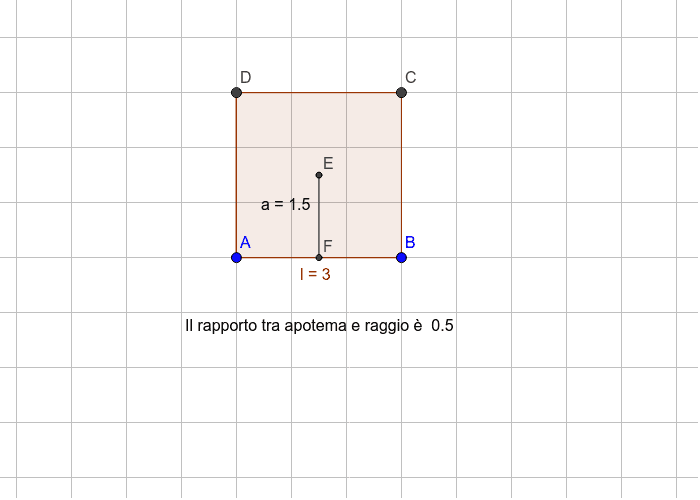
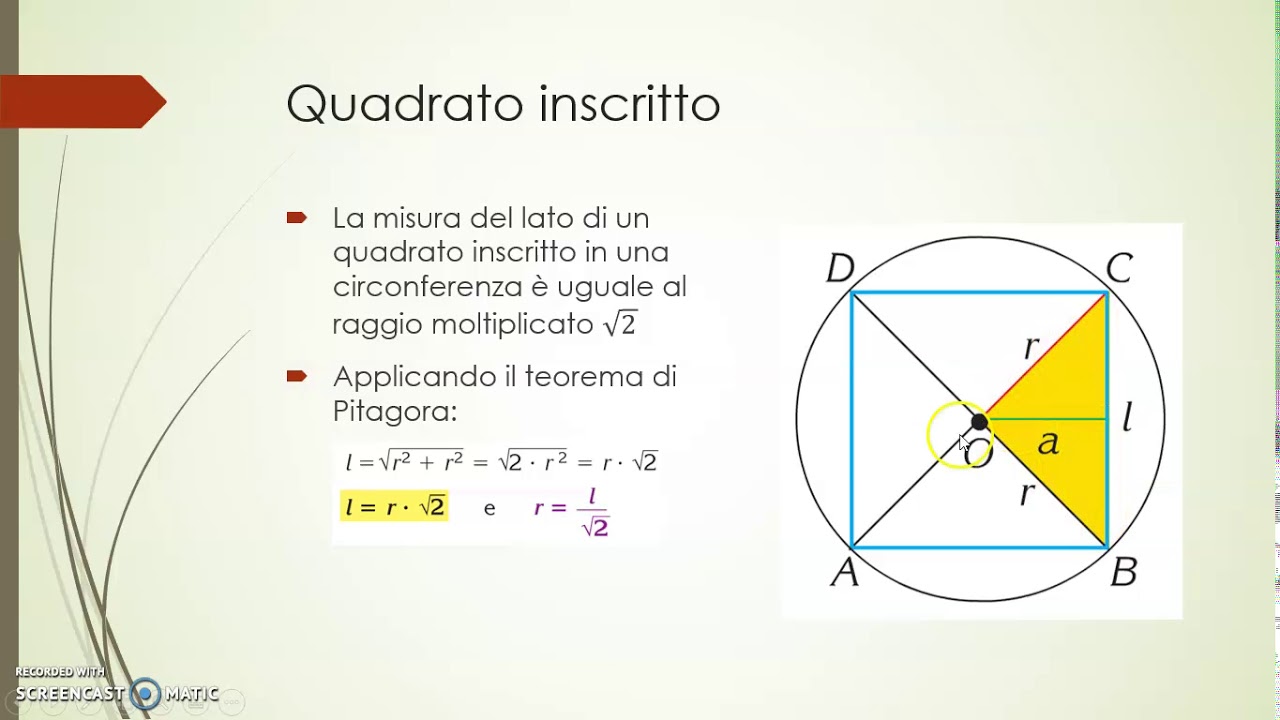
L area invece si calcola moltiplicando il perimetro per l apotema e dividendo per due oppure moltiplicando il quadrato del lato per un fattore che dipende dal. Area e lunghezza laterale. Il suo utilizzo principale è nel calcolo delle aree combinato al perimetro in quanto coincide pure con l altezza degli n triangoli isosceli congruenti in cui è divisibile il poligono. L apotema di un quadrato è il raggio della circonferenza inscritta al quadrato e ha misura pari a metà di quella del lato.

Se ne deduce che se siete a conoscenza del lato del quadrato vi sarà facile calcolare l apotema utilizzando la seguente formula. Trova la lunghezza dell apotema prendendo la radice quadrata del risultato dal passaggio 5. Nel caso di un quadrato questo passaggio può sembrare superfluo ma è necessario soprattutto per molti poligoni lati. Ciascun poligono regolare ammette una circonferenza circoscritta e una circonferenza inscritta che hanno il medesimo centro.

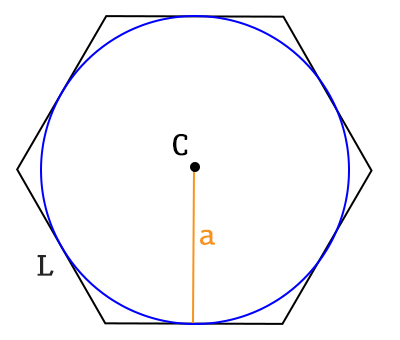
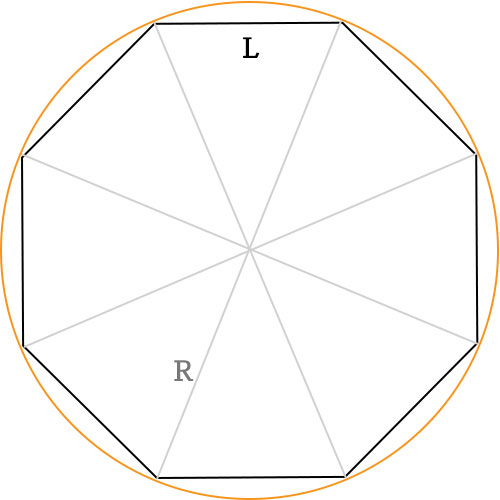
R raggio della circonferenza circoscritta. Tra i poligoni regolari più comuni troviamo il triangolo equilatero e il quadrato nei problemi di geometria ma anche nella vita quotidiana troviamo spesso anche le forme del pentagono regolare dell esagono regolare e dell ottagono regolare. Il rapporto tra apotema e lato è specifico per ciascun poligono regolare e dipende dal numero dei lati. L apotema di un poligono regolare è il raggio del cerchio inscritto.

L area di un poligono regolare si trova moltiplicando la lunghezza del perimetro p per quella dell apotema a e dividendo il prodotto per 2. Completando l esempio la radice quadrata di 9 è uguale a 3 quindi la lunghezza dell apotema è uguale a 3. Indicando con a l apotema e con l il lato per calcolare l apotema del quadrato è sufficiente dividere la misura del lato per 2. A 2 x a.